1-1 数据结构与算法

1.1.1 数据结构

数据结构是讨论计算机系统中数据的存储、组织形式及其相互关系。

数据结构的3个层次：① 数据的逻辑结构；② 数据的存储结构；③ 数据的运算结构(操作集合)。

①逻辑结构	反映数据元素之间的逻辑关系的结构。逻辑关系是指数据元素之间的前后间关系，而与他们在计算机中的存储位置无关。
	线性结构	有且仅有一个开始元素和终点元素; 且所有数据元素最多只有一个直接前趋和一个直接后继。比如线性表。
	非线性结构	一个元素可能有多个直接前趋和多个直接后继。比如树结构、图结构。
②存储结构	数据的逻辑结构在计算机存储空间中的存放形式称为数据的存储结构。 (也称为物理结构)
	反应数据元素在计算机中的存储方案。比如：顺序存储、链接存储、索引存储、散列存储。
③运算结构	数据结构的操作集合
	遍历	在数据结构的各个元素中移动，或查看所有元素。
	插入(增)	往数据结构中添加新的元素。
	删除(删)	把指定的数据结构元素移除。
	更新(改)	修改或替换数据结构中的一个或多个元素。
	查找(查)	在数据结构中找寻满足一定条件的数据元素。
	排序	在保持数据结构中元素个数不变的前提条件下，把元素按照指定的顺序重新排列，排序一般是针对线性逻辑结构。

指为解决特定问题的有穷的操作规则的集合。

算法的 5 个基本特性
①有穷性	有始有终，不会无限循环，且执行时间可接受。
②确定性	算法操作的每一步，其顺序和内容都唯一确定，不会出现二义性。
③数据输入	算法具有0个或多个输入。
④数据输出	算法至少有一个输出。
⑤可行性	算法任一步操作都是可以付诸实践的。

算法点的效率可分为时间效率和空间效率。

空间复杂度 S(n)=O(f(n))	除开存储数据结构本身外（比如指令、常数、变量和输入数据），实现算法所需要的额外辅助空间有多少。
时间复杂度 T(n)=O(f(n))	执行算法所需要的时间以常数时间操作的数量级来表示。相同规模的不同输入，仍可能导致算法的运行时间不同。一般使用算法最坏情况下的的复杂度来做代表。
	常数时间操作是指我们在写代码的时候会涉及到一些指令,这些执令都是固定时间的操作。这些指令是和数据量没有关系的,比如加、减、乘、除、模、位移运算,又或者数组的寻址。
	不同的机器常数时间操作不一样，比如新一代的机器可能性能更好，常数时间操作更短。但是我们用常数时间操作的数量级（而非具体的数值）来衡量时间复杂度的话，就可以忽略机器的因素，而聚焦到算法本身上来。
	时间复杂度可以用T(n)的自然特性加以区分，如下：
	常量时间 O(1)	线性时间 O(n)	对数时间 O(logn)	指数时间 O(n**2)

Python 中的 timeit 模块可以来测试代码的执行时间，网上有很多资料,这里不赘述。
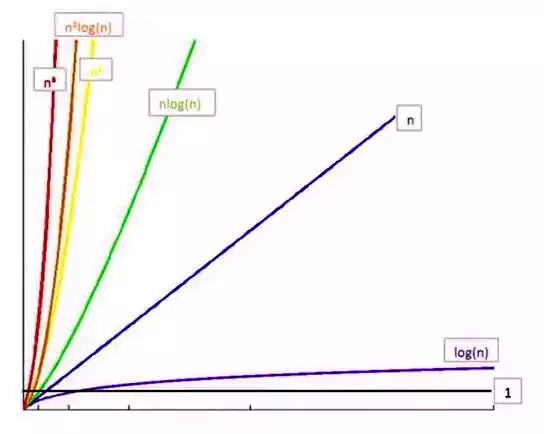
时间复杂度大致上有以下的大小关系：

O(1) < O(logN) < O(logN^2) < O(N) < O(N*logN) < O(N^2) < O(N^3)< …<O(N^k)
… < O( 2^N) < O(3^N) < … < O(k^N) < O(N!)

可以通过数学函数图像来加深理解。

程序 = 算法 + 数据结构 —— 尼古拉斯·沃斯
Algorithm + Data Structures = Programs —— Niklaus Wirth，1984 图灵奖