7-1 树

7-1 树
目录
7.1.1 树结构
7.1.1.1 树的概念
前面讲的都是 线性存储结构,而树是一种典型的非线性存储结构,一个元素可以有多个直接后继元素。
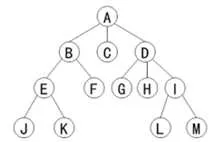
树的一些术语如下所示:
|称呼|含义|
|—-|—-|
|叶子|没有后继结点的 结点称为叶子结点|
|子结点|某一个结点的直接后继结点|
|父结点|某个子结点的直接前驱结点|
|兄弟|具有同一父结点的 一群结点|
|祖先|从根结点开始走到该结点的所有上级结点,都是该结点的祖先|
|结点的度|直接后继结点的数目(子结点数目)|
|结点的层次|根结点为1,其它结点的层次等于它的父结点层次+1|
|树的深度|结点的最大层次值|
|森林|不同的树的集合;如果一棵树删除了根结点,那么剩下的子树就组成一片森林|
7.1.1.2 争议问题
关于树的根结点的数目的问题
这个似乎一直以来都有点矛盾,不同的书上可能说的不一样。
有的书说,树有且只有一个根结点,即根结点数目为1;有的书说,树的根结点可以为0,这时候称为空树。
而且连网上的各种资料也都存在这两种说法:
维基百科截图如下:
还是维基百科:
按照这里的说法: 二叉树结点可以为0,普通树不行;
那么,二叉树是不是树???二叉树当然是树。所以要说【树的结点】最小可以是1还是0呢?这里感觉说法确实很难自洽。
那就看具体情况来回答这个问题吧,也不用过多纠结。
7.1.1.3 树的种类
树依据不同的划分基准可以分为很多种类,这里大致罗列出常见的一些,并不完整,只是作为基本了解:

7.1.2 二叉树
本文简要介绍几种常见的二叉树。简单地理解,满足以下两个条件的树就是二叉树:
①本身是有序树(区分左右)!!!
②树中包含的各个结点的度不能超过 2,即只能是 0、1 或者 2;
7.1.2.1 满二叉树
| 定义 | 如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。 |
| 性质 | ①满二叉树中第 k 层的结点数为 2^ (k-1) 个。(假设根结点层数是1) |
| ②深度为 k 的满二叉树必有 2^k - 1 个结点(等比数列求和公式) ,叶子数为 2^ (k-1)。 | |
| ③满二叉树中不存在度为 1 的结点,每一个分支点都有两棵深度相同的子树,且叶子结点都在最底层。 | |
| ④具有 n 个结点的满二叉树的深度为 log2(n+1) |
7.1.2.2 完全二叉树
| 定义 | 二叉树中 除去最后一层结点 为满二叉树,且最后一层的结点依次从左到右有序分布; 或者这么理解:一个具有n个结点的二叉树,如果其结点编号 和 一颗满二叉树的1---n个结点的编号完全一致,那这棵树就是完全二叉树。 |
| 性质 | ①N 个结点的完全二叉树的深度为 ⌊log2 N⌋+1。(向下取整再加1) |
| ②如果将含有的结点按照层次从左到右依次标号,对于任意一个结点 i 完全二叉树,有以下几个结论成立:
(首先假设i=0 时,表示的是根结点,无父亲结点;在python中,往往是索引从0开始计数) a. i>0 时,父亲结点为结点 [(i-1)/2] (向下取整)。 (在实际python的code中,用int取整即可,如果使用//向下取整,会在-0.5时取到-1,当i=0时使用//无法正确取数,所以用int向靠近0取整,能将i=0也直接统一进来) b. i 结点的左孩子( 如果有的话 )是结点 2*i +1 。 c. i 结点的右孩子( 如果有的话 )是结点 2*i +2。。 |
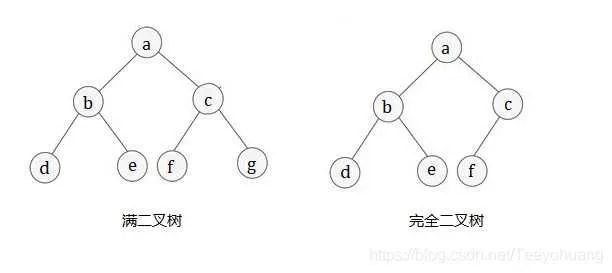
在讲排序部分和优先队列的时候,遇到的大根堆/小根堆,就是属于完全二叉树;
大根堆:根结点是整棵树的最大值;并且对于每一棵子树而言,其最大值也都在子树根结点
小根堆:根结点是整棵树的最小值;并且对于每一棵子树而言,其最小值也都在子树根结点
7.1.2.3 排序二叉树(二叉查找树、二叉搜索树)
又称二叉查找树(Binary Search Tree - BST),亦称二叉搜索树。
定义为:一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树。
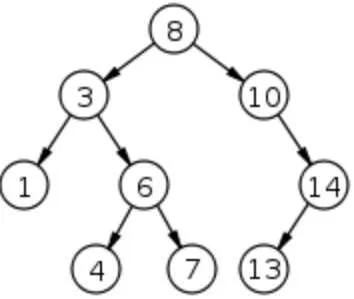
二叉搜索树有着高效的插入、删除、查询操作。
平均时间的时间复杂度为 O(log n),最差情况为 O(n)。
二叉搜索树与堆不同,不一定是完全二叉树,底层不容易直接用数组表示,一般是用链表来进行构造的;
其实二叉搜索树查找元素的过程,就是在实现“二分查找”。
7.1.2.4 平衡二叉搜索树
平衡二叉搜索树又被称为 AVL树,是 Adelson-Velsky and Landis Tree的缩写,分别是两个提出者的名字。
其实是对普通二叉搜索树的改进。考虑以下情况:
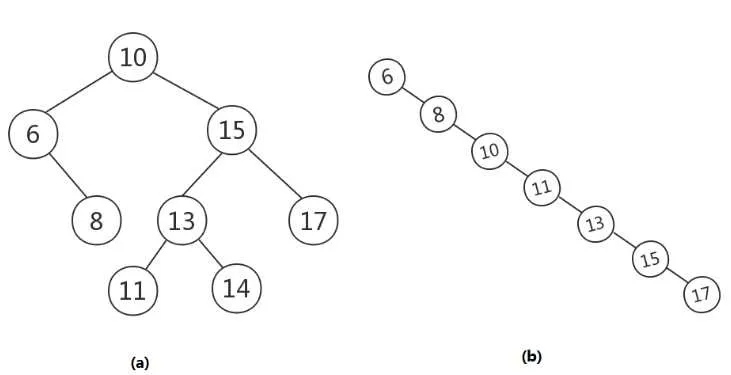
右侧的情况很显然其查找时间是O(N),但它确实是一个二叉搜索树,只是形状太极端了。
可以将其进行改进为AVL树,定义为一棵空树,或者是具有下列性质的二叉树::
(1)本身是一棵二叉搜索树;
(2)每个结点的左右两子树高度差都不超过一;(这就是平衡的含义)
(3)左、右子树也分别为平衡二叉搜索树。
称为平衡二叉搜索树。
平衡二叉搜索树就不会出现上面图(b)的这种极端情况了。
注意:由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树.(下面会提及)
如果应用场景中对插入删除不频繁,只是对查找要求较高,还是可以用AVL树,其查找效率是O(logN)。
7.1.2.4 红黑树
红黑树(Red Black Tree)算是对AVL树进行的一种改进,但是它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉树(AVL),但 对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
红黑树的得名原因是,其结点有颜色之分,分为红色结点和黑色结点,所以每个结点要增加一个存储位表示结点的颜色,其性质如下:
- 每个结点非红即黑.
- 根结点是黑的。
- 每个叶结点都是黑的.(叶子结点是NULL)
- 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
- 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
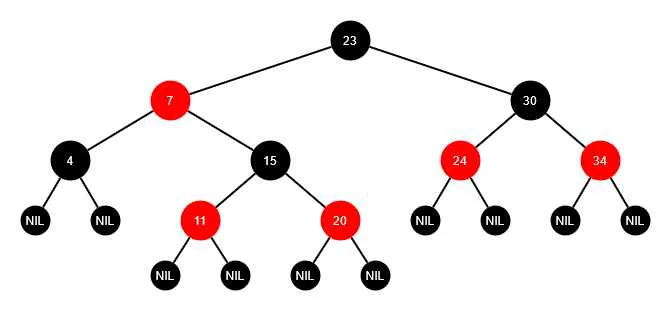
红黑树的一些具体操作不在这里细讲,只需要知道: 它是查找,插入和删除效率都是(logN)。
7.1.3 二叉树的存储结构
7.1.3.1 顺序存储结构
使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。
完全二叉树的顺序存储,仅需从根结点开始,按照层次依次将树中结点存储到数组即可。
如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。方法很简单,人为添加一些并不存在的空结点(其元素值为“空”),使之成为一颗完全二叉树的形式。但是这种方式明显会浪费大量内存,这时就应考虑链式存储方式。
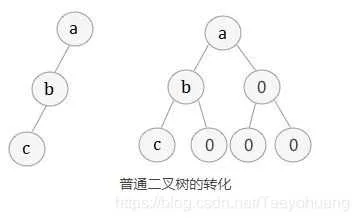
从顺序表中还原完全二叉树也很简单。我们知道,完全二叉树具有这样的性质,将树中结点按照层次并从左到右依次标号(0,1,2,3,…),若结点 i 有左右孩子,则其左孩子结点为 2 i + 1,右孩子结点为 2 i+ 2。此性质可用于还原数组中存储的完全二叉树。
7.1.3.2 链式存储结构
只需从树的根结点开始,将各个结点及其左右孩子使用链表存储即可。不必非得是完全二叉树。下面是二叉树的二叉链表示意图:
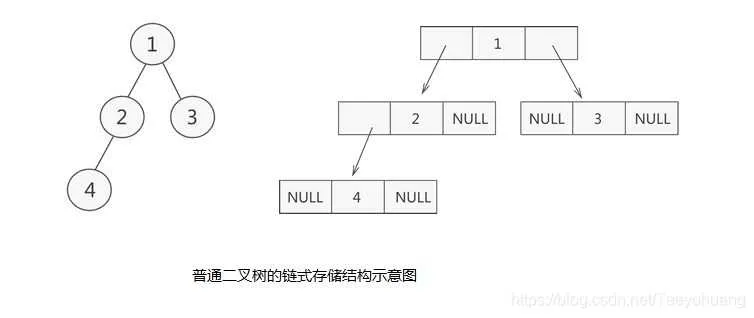
二叉树的结点:
其结点结构由 3 部分构成:
指向左孩子结点的指针(Lchild);结点存储的数据(data);指向右孩子结点的指针(Rchild)
这样的链表结构,通常称为二叉链表。
class BiTNode(object): |
7.1.4 二叉树的遍历方式
7.1.4.1 深度优先遍历
深度优先搜索(Depth First Search - DFS)是沿着树的深度遍历树的结点,尽可能深的搜索树的分支。
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的结点,它们之间的不同在于访问每个结点的次序不同。这三种遍历分别叫做先序遍历(preorder),中序遍历(inorder)和后序遍历(postorder)。
7.1.4.1.1 先序遍历
在先序遍历中,我们对每一棵子树,都是先访问其根结点,然后访问其左孩子结点,最后访问其又孩子结点。
路径为:根结点->左子树->右子树
'''递归法''' |
7.1.4.1.2 中序遍历
在先序遍历中,我们对每一棵子树,都是先访问其左子结点,然后访问其根结点,最后访问其右孩子结点。
路径为:左子树->根结点->右子树'''递归法'''
# 递归法就是调用系统栈
def inorder(node):
if not node:
return
inorder(node.left)
res.append(node.val)
inorder(node.right)
res =[]
preorder(root)
return res
7.1.4.1.3 后序遍历
在先序遍历中,我们对每一棵子树,都是先访问其左子结点,然后访问其右孩子结点,最后访问其根结点。
路径为:左子树->右子树->根结点'''递归法'''
# 递归法就是调用系统栈
def postorder(node):
if not node:
return
postorder(node.left)
postorder(node.right)
res.append(node.val)
res = []
postorder(root)
return res
7.1.4.2 广度优先遍历(层次遍历)
广度优先遍历(Breath First Search - BFS)是横向遍历,即从上到下,一层一层的遍历结点。
'''迭代法''' |



