8-1 图

目录

小节 位置
8.1.1 图的定义
8.1.2 图的分类
8.1.3 图的存储结构
8.1.4 邻接矩阵

8.1.1 图的定义

前面已经讲了 “一对一” 的线性存储结构、”一对多”的树结构 ， 而图结构（Graph）是一种 “多对多“ 的结构；

图G由两个集合 V 和 E 组成， 记为 G=(V, E) ， 其中:
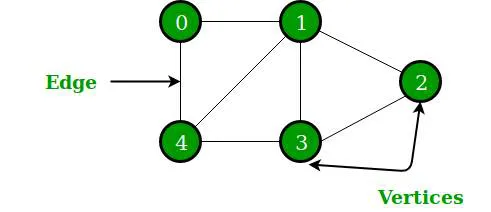
V 是 顶点（Vertex） 的有穷 非空 集合，而顶点通常就是数据结点；
E 是指边 （Edge） 的有穷集合， 边指的是顶点之间的连接关系。

8.1.2 图的分类

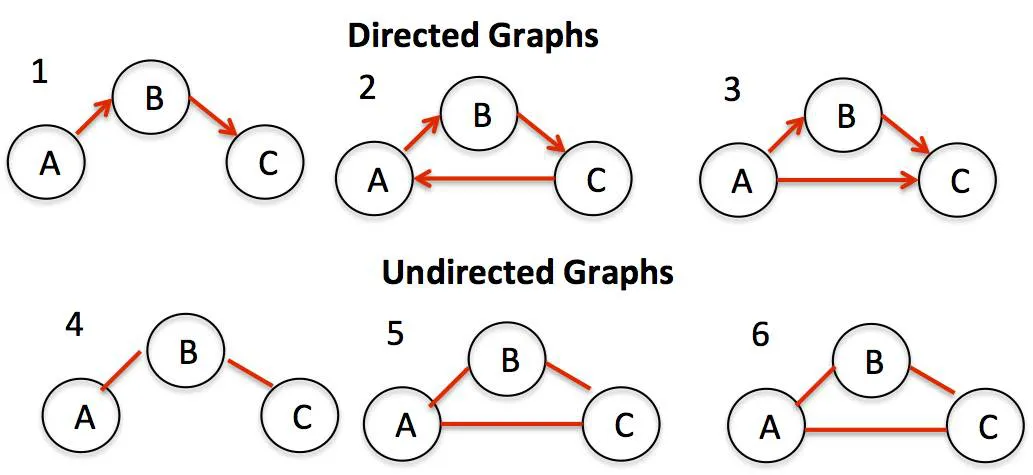
图结构可细分两种表现类型，无向图 （Undirected Graph）和 有向图（Directed Graph）。
若图G的边没有表示方向，则就称为无向图，这样的边用圆括号表示 （Vi, Vj） ；
如果图G中的每条边都是有方向的，就称为有向图，边用尖括号表示 < Vi, Vj> ， 表示从 Vi 指向 Vj。

术语 定义
邻接点 对于无向图，每条边的两个端点互为邻接点；
对于有向图， 有向边的终点是 起点的 邻接点，反之不成立！
比如 < u, v> 表示 u指向v， 所以v是u的邻接点， 但 u不是v的邻接点!
弧头和弧尾 有向边也被称为 弧 ，无箭头一端即“起点”称”弧尾“，
有箭头一端, 即“端点”或”弧头“。
度 常用D(V)来表示，在无向图中，顶点的度 就是 以该顶点为端点的边的条数；
在有向图中，指向该顶点的弧的数目 称为 入度ID(V)， 从该顶点出发的 弧 的数目 称为 出度OD(V)。
有向图的顶点的度是二者之和 D(V) = ID(V) + OD(V).
重要结论： 无论是有向图还是无向图，顶点数n、边数e、和度数之间有关系：所有顶点的度数之和 等于 边数的2倍。
路径和回路 从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。
如果路径中第一个顶点和最后一个顶点相同，则此路径称为”回路“（或”环“）。
若路径 / 回路 中各顶点都不重复，此路径又被称为”简单路径” / “简单回路”
权和网 若图中的每条边（或弧）被赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为”权”，而带权的图通常称为网。

8.1.2.1 细分种类

图又可分为完全图，连通图、稀疏图和稠密图；

名称 定义
完全图 若图中各个顶点都与除自身外的其他顶点有关系，这样的无向图称为完全图。同时，满足此条件的有向图则称为有向完全图。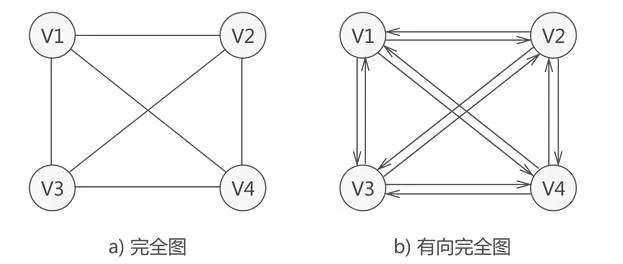
稀疏图和稠密图 这两种图是相对存在的，即如果图中具有很少的边（或弧），此图就称为”稀疏图”；反之，则称此图为”稠密图”。
稀疏和稠密的判断条件是：e < nlogn，其中 e 表示图中边（或弧）的数量，n 表示图中顶点的数量。如果式子成立，则为稀疏图；反之为稠密图。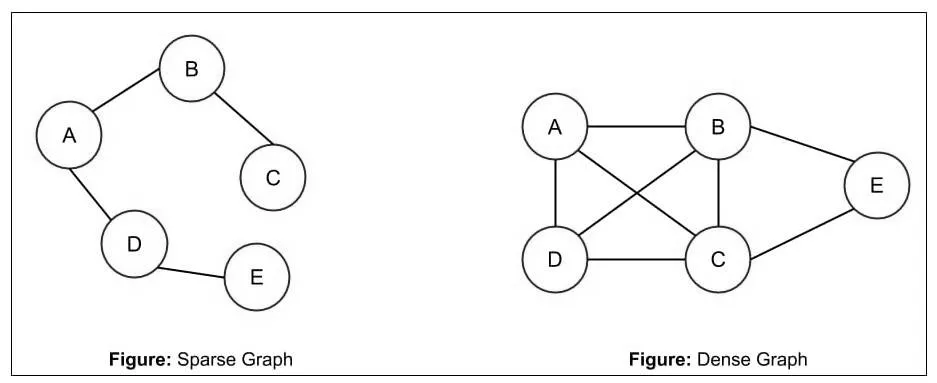
连通图 在无向图中，若每一对顶点 u和v之间都能找到一条路径，则此图称为 连通图；
若无向图不是连通图，但图中存储某个子图符合连通图的性质，则称该子图为连通分量。（这里的子图指的是图中”最大”的连通子图）
在有向图中，若每一对顶点u和v之间都存在 u到v 以及 从 v到u的路径，则成为强连通图。
若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量。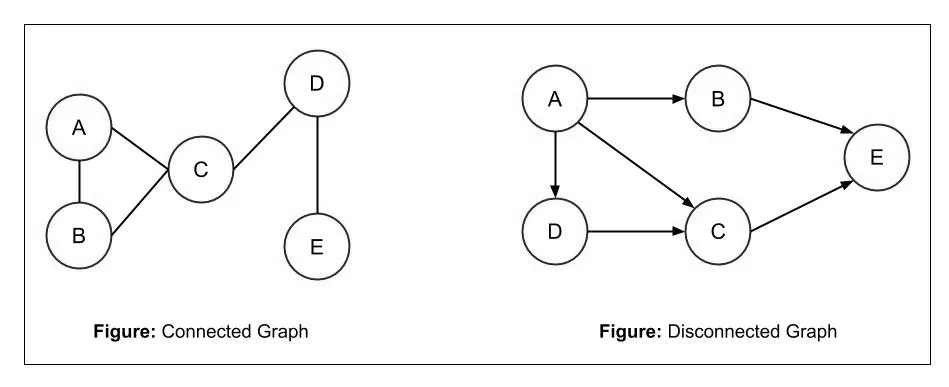
加权图 图中的边带有权值：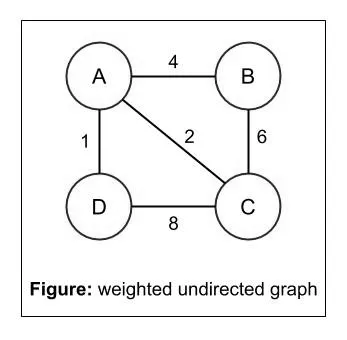

8.1.3 图的存储结构

8.1.3.1 邻接矩阵

图结构的元素之间虽然具有“多对多”的关系，但是同样可以采用顺序存储，即使用数组有效地存储图。

集合V中所有的顶点可以利用一个一维数组存储；
而集合E中所有的边可以用一个二维数组来存储，此二维数组就称为 邻接矩阵！
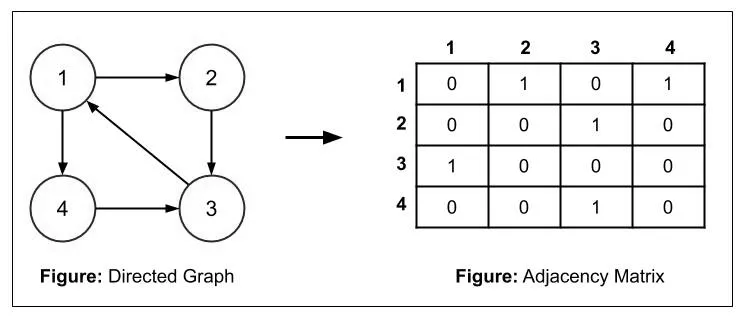
如下图所示, 点与点之间如果有边存在, 那矩阵中对应位置的值就为 1；反之为 0.

|

设 $G=(V,E)$ 是有 n 个（n>=1）顶点的 ==有向图== ，则G的邻接矩阵是具有如下性质的 n x n 矩阵：

设 $G=(V,E)$ 是有n个（n>=1）顶点的 ==无向图==，则G的邻接矩阵是具有如下性质的 n x n 矩阵：

  • 对于无向图，邻接矩阵第 i 行（或第 i 列）的元素之和是 顶点 $V_i$ 的度；
  • 对于有向图，邻接矩阵第 i 行 元素之和为 顶点Vi的出度， 邻接矩阵第 i 列 的 元素之和 为顶点 $V_i$ 的入度。
    比如上图的有向图的邻接矩阵中，第3行的和为1：表示顶点3的出度为1；第3列的和为2：表示顶点3的入度为2.
  • 对于带权图，也就是 网 来说， 只需要把上面的 等于 1 的情况改为 权重 $W_{ij}$， 把等于 0 的情况 改为 $ \infty $。
  • 容易得出，无向图的邻接矩阵是按矩阵主对角线对称的。

8.1.3.2 邻接表

邻接表既适用于存储无向图，也适用于存储有向图。邻接表存储图的实现方式是，给图中的每个顶点独自建立一个链表，第 i 个单链表中的结点包含顶点 i 的所有邻接点。

为了便于管理这些链表，通常会将所有链表的头结点存储到数组中（也可以用链表存储）。
也正因为各个链表的头结点存储的是各个顶点，因此各链表在存储邻接点数据时，仅需存储该邻接顶点位于数组中的位置下标即可，不用存储完整的顶点数据，降低了空间复杂度；同时知道点的下标，就能以O(1)的时间复杂度从数组中获得顶点数据。

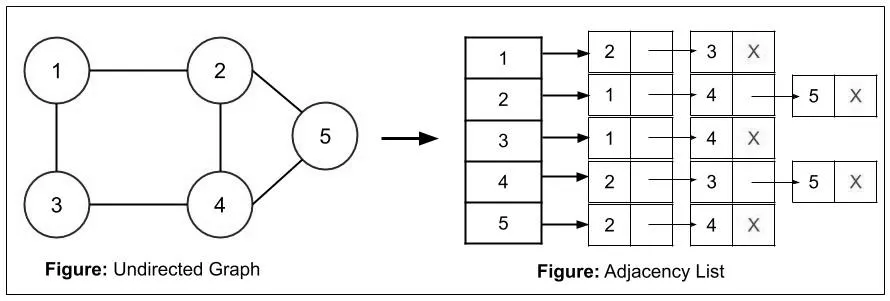
假设该图是 G(n, m) 。这里 G 是图， n 是结点数， m 是图 G 中存在的边的总数 。
在无向图的情况下，链表的结点总数将为 2m （因为连接是双向的）；使用的总空间为 O(n + 2m)。
在有向图的情况下，使用的总空间为 O(n + m)。


对于稀疏图，推荐使用邻接表，因为稀疏矩阵会浪费大量内存；
对于稠密图，可以使用邻接矩阵。

8.1.4 图的遍历

图的遍历可以分为深度优先遍历和广度优先遍历，和树的深度优先遍历和广度优先遍历十分相似。

我在 BiliBili 上看到一个讲解视频，讲得十分详尽，所以这里直接引用该视频的链接，已获得原视频up主：码农论坛 的授权，同时原视频地址也备注在下方。

8.1.4.1 图的深度优先遍历

原视频地址：link

下面用一个例子演示深度优先遍历的 code，假设有图结构如下：

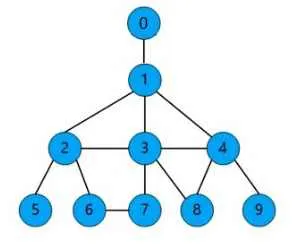
'''上图中的graph用列表表示如下
索引代表结点, 
列表中的子列表代表当前结点的邻接点'''
graph = [
    [1],
    [0,2,3,4],
    [1,3,5,6],
    [1,2,4,7,8],
    [1,3,8,9],
    [2],
    [2,7],
    [3,6],
    [3,4],
    [4]
]

# 深度优先遍历的code如下

def DFS(node):
    # 终止条件：当前结点已经被访问过
    if node in visited:
      return 

    # 将当前结点加入结果中
    res.append(node)
    # 同时记录当前结点已经被访问的状态
    visited[node] = True

    # 遍历当前结点的邻接点
    for neighbour in graph[node]:
        # 假设这里 graph[node] 存储的是 node 的邻接点
        # 具体的题目中这里的写法可能稍有不同
        DFS(neighbour)

    return

visited = {} # 记录哪些结点已经被访问的哈希表
res = [] # 存储遍历结果的list
DFS(0)
print(res)

其实图的深度优先遍历，和树的深度优先遍历中的【先序遍历】是很相似的，他们的核心流程基本一致；用伪代码表示如下：

def DFS(node):
    # step 1. 终止条件
    if End_Condition:
      return
    
    # step 2. 访问当前结点
    visit(node)

    # step 3. 利用递归操作，访问当前结点的相关结点
    DFS(node_relations)
  
    return

这里再贴上二叉树的先序遍历的code用于对照理解：

def preorder(root):
    if not root:
        return
    # 对每棵子树的结构，都先访问根结点的值
    res.append(root.val)
    # 然后递归地分别处理左右子结点
    preorder(root.left)
    preorder(root.right)

res =[]
preorder(root)
return res
二叉树先序遍历 图的深度优先遍历
step 1 终止条件为node为空 当前结点已经被遍历
step 2 访问当前结点 访问当前结点
step 3 利用递归, 访问当前结点的子结点 利用递归，访问当前结点的邻接点

需要注意的有几点

  • 树的遍历一定是从root结点开始，所以用同一种方法遍历得到的list是唯一确定的；
    而图的遍历，起始位置不确定，通常可以从任何一个点开始遍历，所以即便用同一种方法，如果选取不同的起始点，得到的遍历结果的顺序也不一样；

  • 上面的例子只是比较简单的情况，它是一个连通图；
    还有非连通的情况，比如两棵不同的树就是一个非连通图，对于每一个连通分量的遍历，依然可以使用上面的code示范的方法，只不过对于不同的连通分量的切换，还需要额外处理，可以自己思考一下，此处不再赘述。

8.1.4.2 图的广度优先遍历

原视频地址：link

下面用一个例子演示深度优先遍历的 code，假设有图结构如下：

def BFS(graph, node):
    if len(graph) == 0:
        return []
    
    # 将初始结点先入队
    q, res = [node], []
    # 凡是入队的结点, 就要标记为访问过
    visited = {node:True}
    while q:
        layer = []
        # 这个 n 其实就是在求要遍历的那一层的宽度
        n = len(q)
        for i in range(n):
            node = q.pop(0)
            # 队列中弹出的元素直接放入该层的list中
            layer.append(node)
            # 对该结点的邻接点进行入队操作
            for neighbour in graph[node]: 
                # 要判断邻接点是否已经被访问过
                if neighbour not in visited:
                    # 没被访问过的邻接点： 入队 + 标记状态
                    q.append(neighbour)
                    visited[neighbour] = True
        res.append(layer)
    
    return res

print(BFS(graph, 0))
print(BFS(graph, 9))

关于层次遍历，其实就是看结点距离起始点的路径有几段，
以起始点为9 为例：
第一层就是 [9]；
第二层就是距离9的路径为1段的 [4]
第三层就是距离9的路径为2段的 [1, 3, 8]
第四层就是距离9的路径为3段的 [0, 2, 7]
第五层就是距离9的路径为4段的 [5, 6]

图的知识点其实还有很多，但是作为基础的算法结构来讲，了解到图的遍历就基本可以了。