2 卷积与池化

深度学习系列博文目录一览
————————————————
2 卷积与池化
这里暂时不介绍卷积操作具体是如何进行的,关于这点,很多文章都有介绍。
本文主要介绍一下 为何会广泛使用卷积操作?
参考资料:
《Deep Learning》
卷积运算 主要通过三个重要的思想来帮助改进机器学习系统:
稀疏交互 sparse interactions
参数共享 parameter sharing
等变表示 equivariant representations
2.1 稀疏交互
卷积网络的稀疏交互 - sparse interactions(也叫稀疏连接 或者 稀疏权重),是通过使卷积核的大小远小于输入的大小来达到的。这就区别于全连接层的 矩阵相乘运算,
卷积核的话就只接受有限个输入,使得参数量减小。</font>比如3x3大小的卷积核,就只接受9个像素点上的输入。这块儿大小有个更专业的术语,叫做 感受野(receptive field),或者FOV(field of view).但是这样说明卷积核主要是在学习局部相关性。
CNN中的卷积操作在对图像进行处理时,主要是为了获得图片局部特征,在计算机视觉里,我们将这样的操作叫做滤波,都是为了获得局部领域的输出。常用的卷积操作本质上就是加权平均,这样的线性运算是获取局部特征最简单的操作,利用BP算法也显得特别直接。
CNN同样可以处理时间序列和文本数据,因为CNN利用的就是数据的局部相关性,语音和文本具备局部相关性。
2.2 参数共享
参数共享 - parameter sharing ,是指 在一个模型的多个函数中使用相同的参数。卷积网络中,一般情况下一个卷积核会作用在输入的每一个位置,这种参数共享保证了我们只需要学习一个参数集合,而不是对每一个输入位置都需要学习一个单独的参数。
通俗来讲,就是我们在运用卷积操作时,通常情况(因为也有一些特殊情况)下,是用一个卷积核 从左往右、从上到下 按照步长stride,去遍历完特征图的所有位置。
2.3 等变表示
参数共享使得神经网络层对平移具有等变性质。
所谓等变,即对其输入施加的变换也会同样反应在输出上。
即如果对输入进行轻微的平移,卷积运算得到的结果在忽略位置的时候,是一样的。
比如若图像上的一个特征本来位于图像左侧,现在将该区域平移到右侧,卷积网络依然能够检测到该特征,只不过探测到的位置会发生变化而已。更具体一点,如果一个图像上有一只小狗位于左侧,现在将小狗的区域平移到图像右侧去,卷积网络依然能够检测到这个区域的特征,并且判定该特征是一只小狗。
但是卷积对其他的一些变换并不是天然等变的,例如对于图像的放缩或者旋转变换,需要其他的一些机制来处理这些变换。
2.4 常规卷积与其他卷积的对比
①常规卷积
可以看作只有一个核,且被应用到各个位置。
相当于每个位置对应的卷积核的参数都是一样的,这就是前面说到的参数共享。
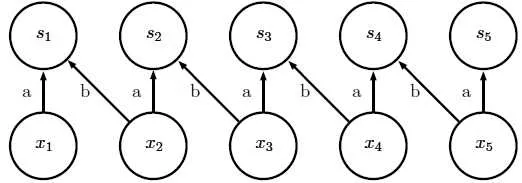
图中S为卷积核;x为特征值;每个卷积核接受2个位置的输入,
但是参数a,b一直在重复使用,相当于是同一个卷积核在从左往右遍历</i>
②局部连接
注意:有些地方提及的局部连接,是指的本篇博文中的第1点,稀疏交互,
本篇博文的名称规则是依据DeepLearning这本花书来的,这里讲的局部连接是指的非共享卷积。
局部连接有时候也称为非共享卷积,因为它和具有一个小核的离散卷积运算很像,但并不横跨位置来共享参数,也就是说,并不是一个卷积核 作用于所有的输入位置,而是不同的输入位置所对应的卷积核 拥有不同的参数。
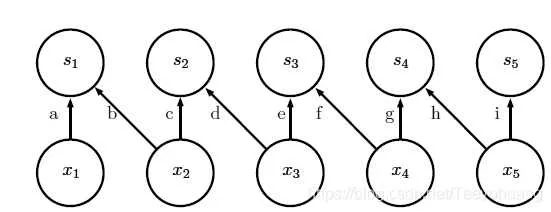
图中S为卷积核;x为特征值;每个卷积核都有各自的参数。
③平铺卷积
是介于局部卷积 和 标准卷积之间,与局部卷积相同的地方在于,相邻的单元具有不同的参数,与其区别在于, 会有 t 个不同的卷积核循环使用,也就是说相隔为 t 的卷积核,就会共享参数。
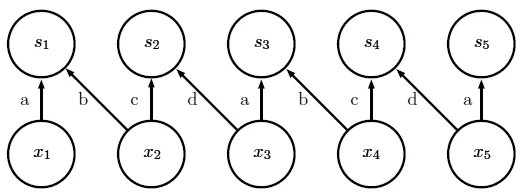
图中S为卷积核;x为特征值;相邻的卷积核都有各自的参数;
但每隔 t 个(图中 t=2)卷积核,参数就会重复使用。</i>
④全连接层
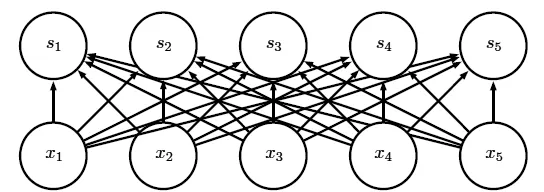
图中S为卷积核;x为特征值;每条边都有各自的参数,但是它的感受野是全部的x特征,并不是局部的连接。
2.5 池化操作
池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。比如最大池化、平均池化等等。
不管采用什么样的池化函数,当输入作出少量平移时,池化能够帮助输入的表示近似不变(invariant)。
对于平移的不变性是指当我们对输入进行少量平移时,经过池化函数后的大多数输出并不会发生改变。
池化对于不同大小的输入具有重要作用。例如我们想对不同大小的图像进行分类时,分类层的输入必须是固定的大小,而这通常通过调整池化区域的偏置大小来实现,这样分类层总是能接收到相同数量的统计特征。以便于后面的全连接层进行处理
2.6 卷积与池化作为一种无限强的先验
可以把卷积的使用当作是对网络中一层的参数引入了一个无限强的先验概率分布。
这个先验说明了该层应该学得的函数只包含局部连接关系并且对平移具有等变性。
类似的,使用池化 也是一个无限强的先验:每一个单元都具有对少量平移的不变性。
.



