4 激活函数

深度学习系列博文目录一览
————————————————
4 激活函数
激活函数也就是一些非线性单元,如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。如果使用激活函数的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
对于激活函数的使用,可以追溯到多层感知机解决异或(XOR)问题。
参考资料:
4.1 sigmoid
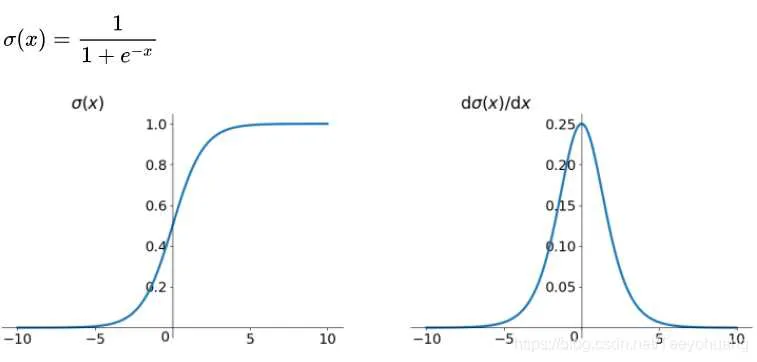
sigmoid作激活函数的优点:
梯度计算较为方便
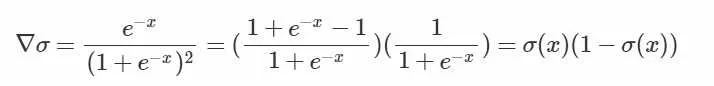
能够控制数值的幅度
(即能压缩数据,在深层网络中可以保持数据幅度不会出现大的变化,保证数据幅度不会有问题)
sigmoid缺点:
容易出现梯度消失(gradient vanishing)的现象:
当激活函数的输入值接近饱和区(两边)时,变化太缓慢,导数接近0;根据反向传播的数学依据是微积分求导的链式法则,当前导数需要之前各层导数的乘积,几个比较小的数相乘,导数结果很接近0,从而无法完成深层网络的训练。
Sigmoid的输出不是0均值(zero-centered)的:
输出值恒大于0,这会导致模型训练的收敛速度变慢。比如上一级 经过 sigmoid之后,输出的一定是个正数x,那么希望更新这一级的参数的时候,wx+b,w的梯度是x,但是x恒为正,那么我这一级的w(w是个向量,里面会有很多分量)的所有分量都只能往正向移动,不能各个分量朝不同的方向移动,所以收敛速度变慢。幂运算相对来讲比较耗时。
4.2 tanh
tanh读作 Hyperbolic Tangent
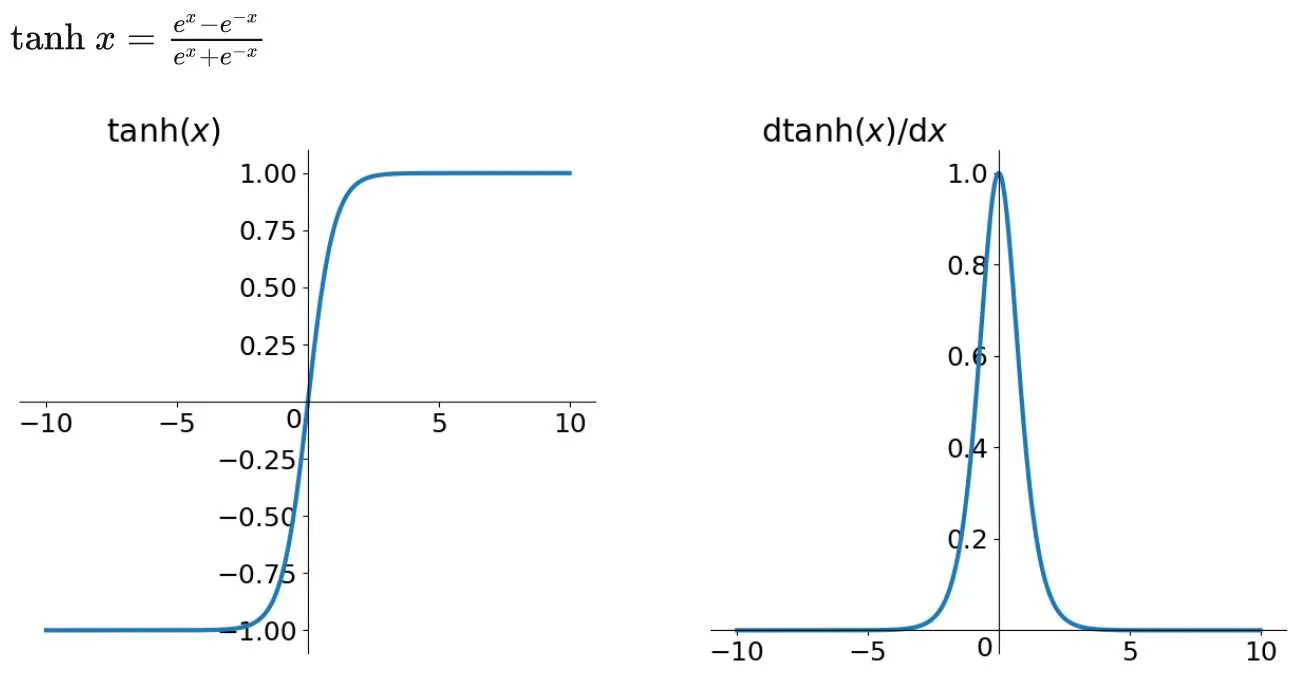
它的输出是0均值的了,解决了上面sigmoid的(2问题),但是梯度消失 和 幂运算费时的问题依然存在。
4.3 ReLU
ReLU(Rectified Linear Unit):整流线性单元
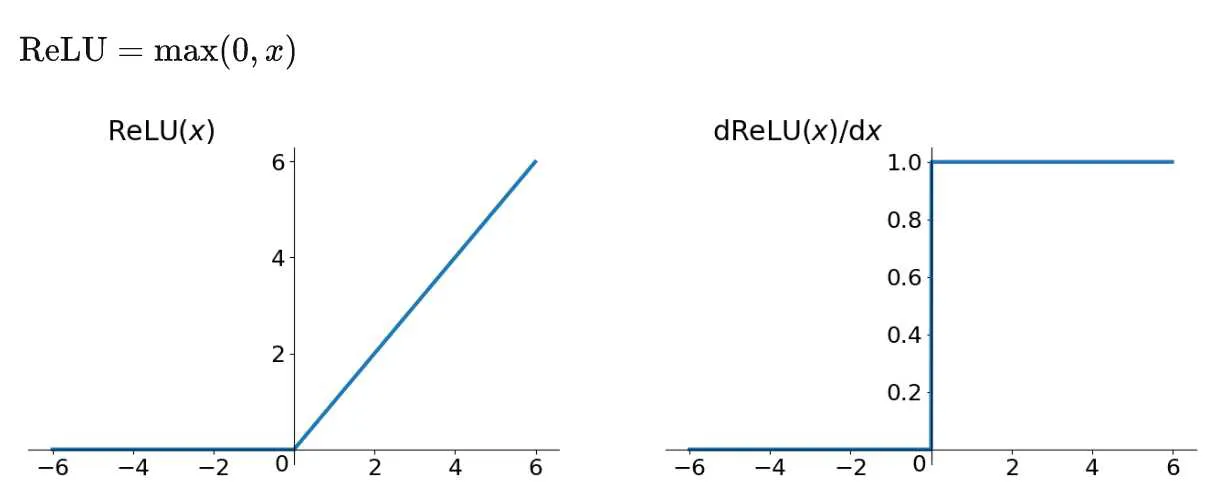
ReLU函数其实就是一个取最大值函数,注意这并不是全区间可导的(0点不连续),但是我们可以取sub-gradient,如上图所示。ReLU虽然简单,但却是近几年的重要成果,有以下几大优点:
- 解决了gradient vanishing问题 (在正区间)
- 计算速度非常快,只需要判断输入是否大于0
- 收敛速度远快于sigmoid和tanh
ReLU也有几个需要特别注意的问题:
ReLU的输出不是zero-centered
Dead ReLU Problem
指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生:
(1) 非常不幸的参数初始化,这种情况比较少见 ;(2) learning rate太高导致在训练过程中 参数更新太大,使得输入发生巨大变化后越过0界,则前向传播为0,相当于这个单元被关闭了,反向传播的时候也为0 ,这个关掉的单元就跳不出来了。解决方法是可以采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
尽管存在这两个问题,ReLU目前仍是最常用的activation function,在搭建人工神经网络的时候推荐优先尝试!
4.4 Leaky ReLU
中文称作:渗漏整流线性单元
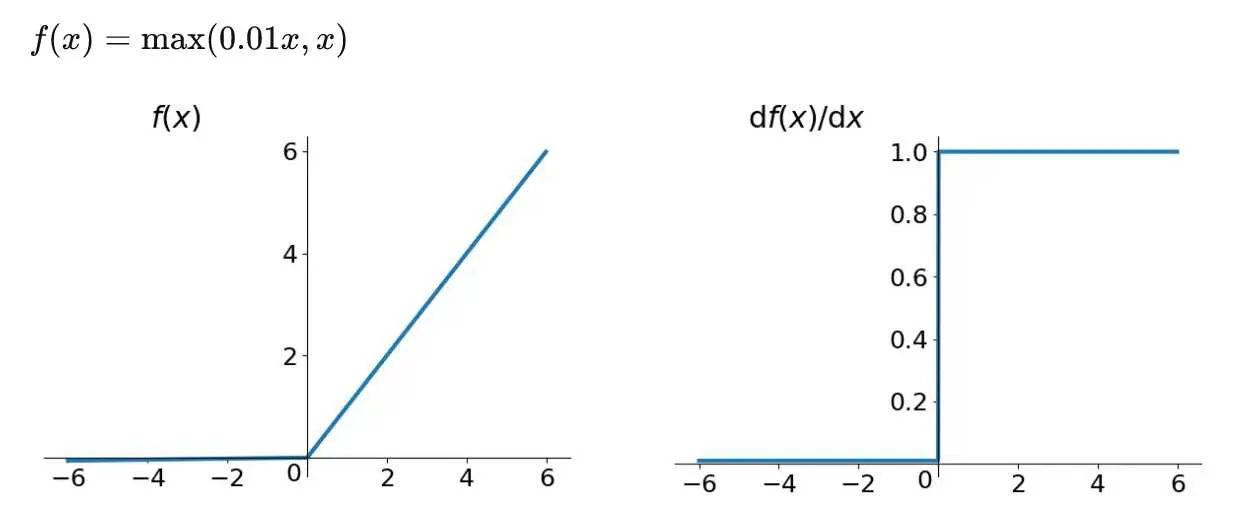
为了解决Dead ReLU Problem,提出了将ReLU的前半段设为0.01x而非0.
4.5 ELU
ELU (Exponential Linear Units):指数化线性单元
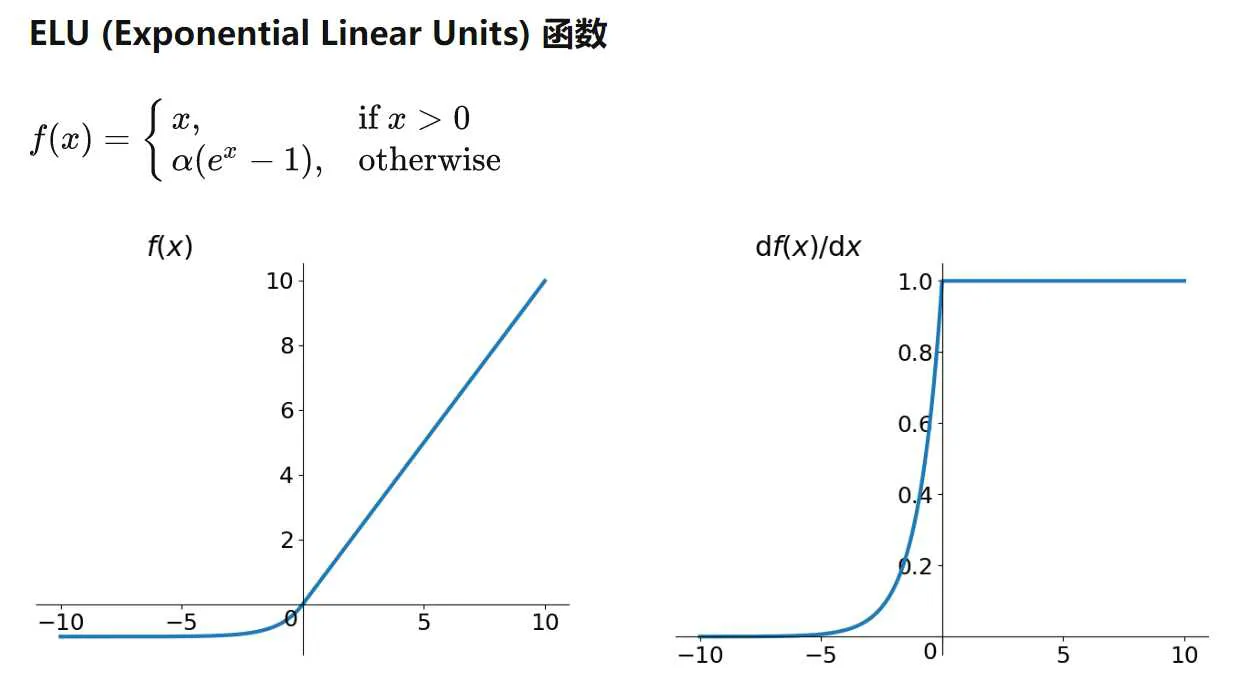
ELU也是为解决ReLU存在的问题而提出,显然,ELU有ReLU的基本所有优点,以及:
(1)不会有Dead ReLU问题
(2)输出的均值接近0,zero-centered
它的一个小问题在于计算量稍大。类似于Leaky ReLU,理论上虽然好于ReLU,但在实际使用中目前并没有好的证据ELU总是优于ReLU。
4.6 PReLU
PReLU ( Parameterized ReLU) 参数整流线性单元
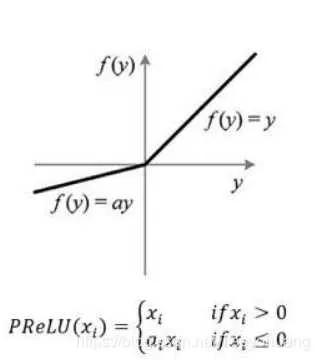
从形式上看,很像Leaky ReLU,但是区别在于将 PReLU 输入为负半轴部分映射为 一个可学习参数 α 和输入的乘积; Leaky ReLU 而负半轴的参数是一个固定值。
.



