3-监督学习简述

3 监督学习简述
3.1 简介
第1章已经提及,监督学习是 从有标记的训练数据 中学习模式和关系,算法的目标是通过输入特征与其相应的标签之间的关联性,构建一个能够准确预测新数据的标签的模型。
监督学习算法可以分为:分类问题、回归问题和序列标注问题。
3.2 分类问题(Classification)
分类问题是机器学习中很经典的一类问题,它要做的事情是:
所有可能的数据可以被划分为有限个确定的类别,通过监督学习来从数据中学习一个分类模型或分类决策函数,会根据输入数据的特征,预测输入数据属于哪个具体的类别。
这样的模型也被称为分类器。
从上面的定义可以得知,分类器 Y=f(X) 的输出一定是类别,即输出变量 Y 一定是离散值。
而输入变量 X 则没有限制,可以是连续值,也可以是离散值。
机器学习中常见的分类模型有:
>
- 逻辑回归(Logistic Regression)
- 决策树(Decision Tree)
- 支持向量机(Support Vector Machine)
- 神经网络(Neural Network)
- 朴素贝叶斯(Naive Bayes)
3.2.1 常见的分类任务
二分类任务
二分类任务是指的分类的可选类别只有两个,二分类的典型任务有:- 垃圾邮件识别
- 疾病检测
- 信用卡欺诈检测
多分类任务
多分类任务是指的分类的可选类别有多个(但是确定的分类结果只有一个),多分类的典型任务有:- 手写数字识别
- 文本分类
多标签问题
多标签问题是一种特殊的分类问题,与单标签问题不同,它的每个样本可以有多个标签。
在多标签问题中,每个样本与多个类别标签相关联,而不仅仅是一个单一的类别标签。多标签问题的典型应用:- 商品推荐
- 情感分析
- 网页分类
3.2.2 分类问题的评价指标(性能度量)
分类问题的评价指标主要有:
3.2.2.1 准确率(Accuracy)
准确率是指分类器分类正确的样本数占总样本数的比例。假设对于 N 个样本,分类器正确分类的样本数为 P ,则准确率为:
3.2.2.2 错误率(Error Rate)
错误率是指分类器分类错误的样本数占总样本数的比例。假设对于 N 个样本,分类器错误分类的样本数为 F ,则错误率:
3.2.2.3 混淆矩阵(Confusion Matrix)
混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用n行n列的矩阵形式来表示。
混淆矩阵的每一列代表了预测类别,每一列的总数表示预测为该类别的数据的数目;
每一行代表了数据的真实归属类别,每一行的数据总数表示该类别的数据实例的数目。
二分类的混淆矩阵如下图所示:
多分类的混淆矩阵如下图所示: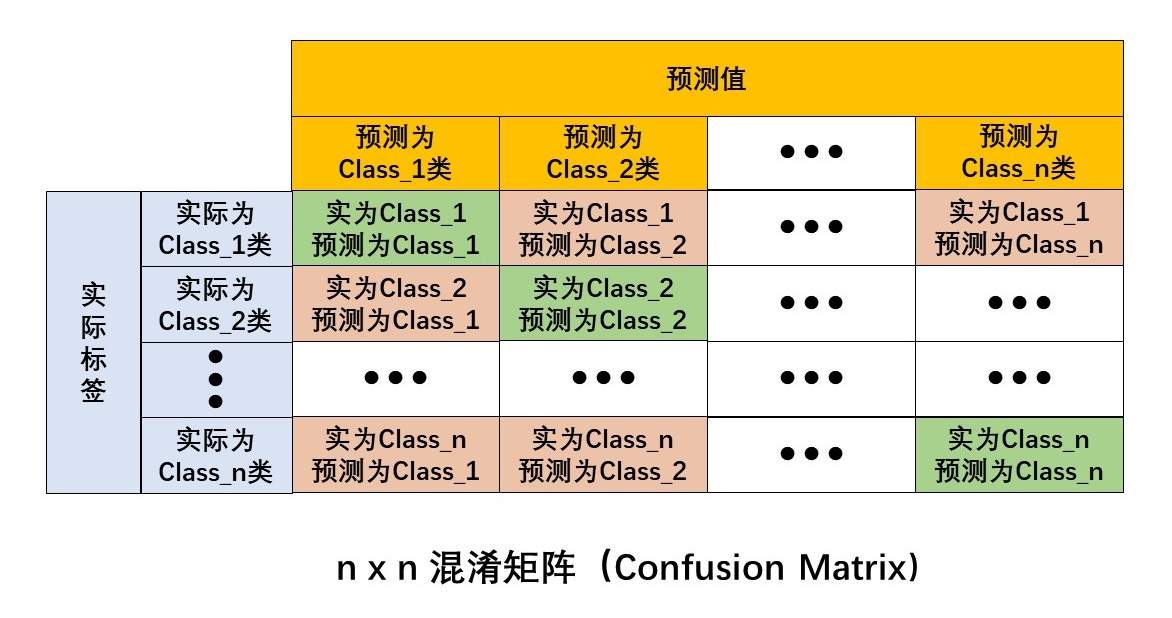
3.2.2.4 精确率(Precision)、召回率(Recall) 和 F1得分
对于二分类问题,由上面提及的二维混淆矩阵可知分类的情况会有以下四种:
| 真阳性 | (True Positive, TP) | 预测为正,实际为正。 |
| 假阳性 | (False Positive, FP) | 预测为正,实际为负。 |
| 真阴性 | (True Negative, TN) | 预测为负,实际为负。 |
| 假阴性 | (False Negative, FN) | 预测为负,实际为正。 |
进而可得以下指标:
精确率(Precision): 预测为正的样本中,实际为正的样本所占的比例。
召回率(Recall): 实际为正的样本中,正确被预测为正的样本所占的比例(正确被预测为正的样本,除以 实际为正的样本)。
精确率也被称为查准率,即检索到的信息中,有多少比例是真正需要的文件。
召回率也被称为查全率,即需要的信息中有多少比例被检索出来了的。
在有些场景下,会提到灵敏度(sensitivity)和特异性(specificity):
特异性(specificity):实际为负的样本中,正确被预测为负的样本所占的比例(正确被预测为负的样本, 除以 实际为负的样本)。与召回率是对偶关系,可以看为“负样本的召回率”。
敏感度(sensitivity):实际为正的样本中,正确被预测为正的样本所占的比例(正确被预测为正的样本,除以 实际为正的样本)。其实和上面的 召回率(recall) 是一个值。
对于精确率和召回率,二者其实是一对充满矛盾的度量,它们之间存在一种此消彼长的关系:
- 一个分类器如果只把可能性大的样本预测为正样本,那么会漏掉很多可能性相对不大但依旧满足的正样本,从而导致召回率降低。
- 如果分类器过于宽松,将很多负样本预测为正样本,那么精确率就会降低。
因此, 可以采用F1得分,是精确率和召回率的调和均值:
F1得分:
将这几个得分指标画在混淆矩阵上如下(图源wikipedia):
3.2.2.5 P-R曲线(Precision-Recall Curve)
上面提到精确率(Precision)和召回率(Recall)存在此消彼长的关系,对于一个分类器,可以画出这两个指标之间关系的曲线图,称为P-R曲线。
对于许多分类器而言,对于每个输入样本,模型都会产生一个输出,这个输出通常表现为一个概率值或得分。这个概率值或得分表示了模型对于这个样本属于某个特定类别的置信度。
例如,在二元分类器中,模型可能会输出一个介于0和1之间的概率值,表示样本属于正类的置信度。在多类分类器中,模型可能会输出一个概率分布,即每个类别的概率值,以便于我们根据这些概率值来决定样本最可能属于的类别。大致情况如下图所示
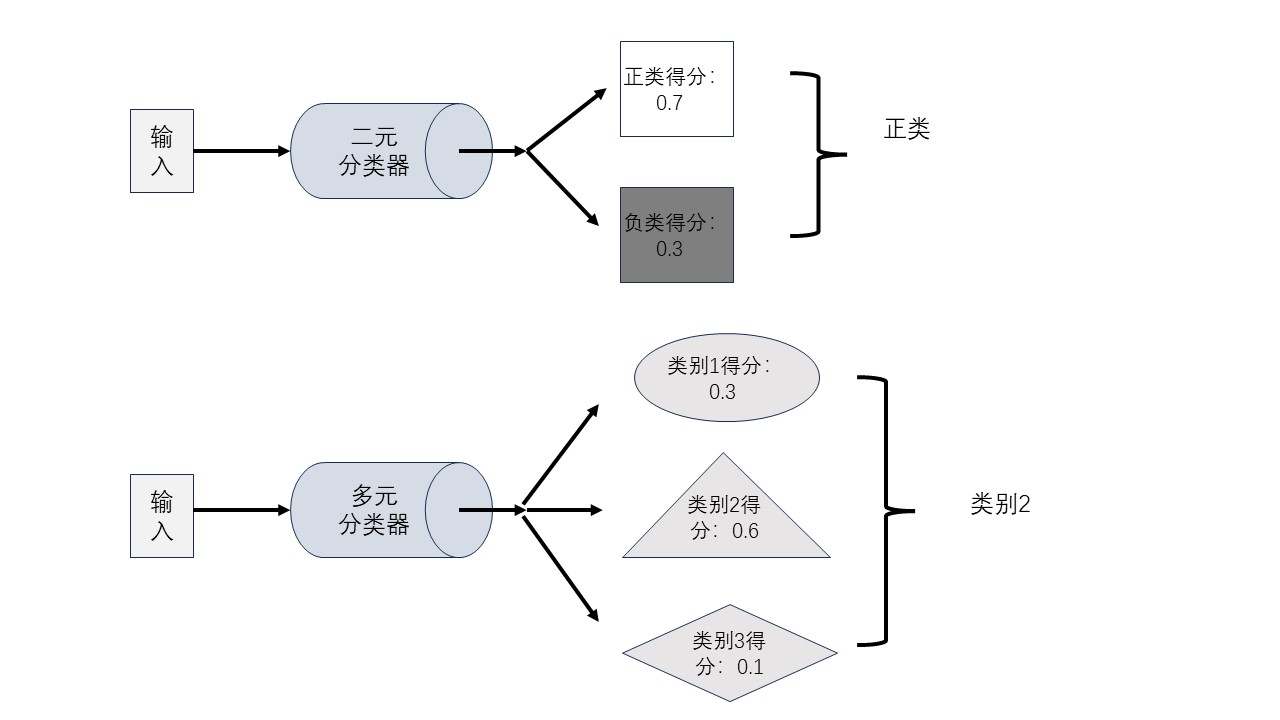
我们可以依据这个分数对样本进行排序,排在越前面的属于正类别的可能性越大,排在后面的属于正类别的可能性越小。此时可以设置一个阈值(Treshhold),当样本的得分大于或等于这个阈值时,就判定样本属于正类别,否则就判定样本属于负类别。
那么,通过不断改变阈值,就可以得到不同的TP、FP、TN、FN,从而得到不同的精确率、召回率;在实际操作时,我们往往直接依次使用样本排序后的得分作为阈值,这样阈值从高到低,得到不同的精确率、召回率,将其画在图中,就可以得到P-R曲线。
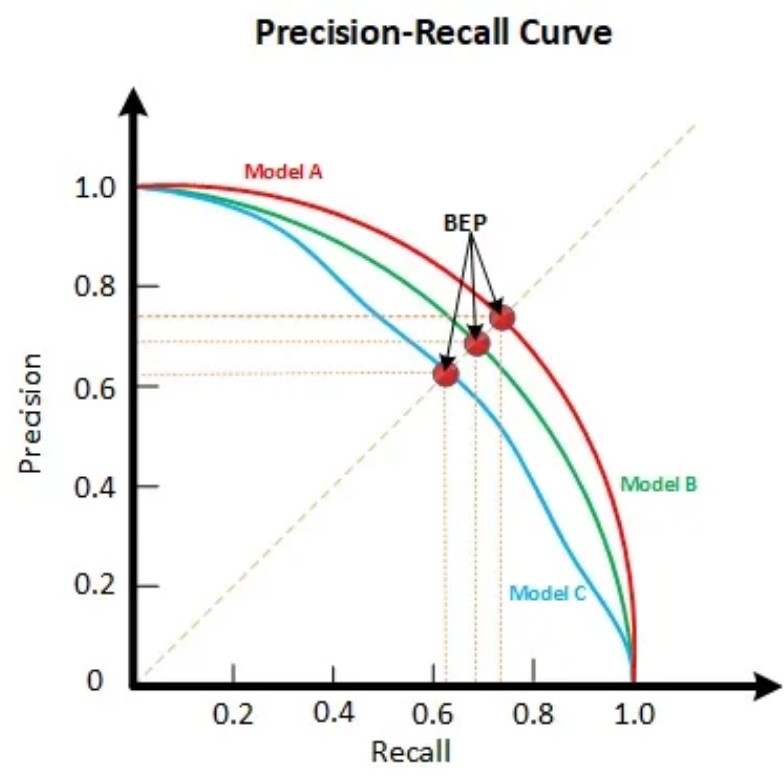
P-R 曲线中,横轴表示召回率,纵轴表示精确率,其曲线所围的面积称为 Average Precision(AP)。
AP值是衡量一个模型在所有阈值下的平均精确率。也就是说,对于同一个数据集,P-R曲线下面积越大的分类器,效果越好。
如果懒得计算P-R曲线所围面积,可以使用BEP点;图中,当Precision = Recall 的点,称为 平衡点(Break-Event Point)。一般来说,BEP点越大,P-R 曲线越凸,则AP值越大,则分类器效果越好。
3.2.2.5 ROC曲线 与 AUC
ROC曲线是P-R曲线的一种变形形式,全称为“(Receiver Operating Characteristic Curve - 接收器工作特征曲线”),(Receiver本意指的是雷达接收器,ROC曲线最早就是应用于雷达目标检测领域),其横轴代表假正例率(False Positive Rate, FPR),纵轴代表真正例率(True Positive Rate, TPR),即:
注:在有的地方,横轴用的是 1-specifity, 事实上,1-specifity = FPR,从上面大的混淆矩阵示意图中就能看到。
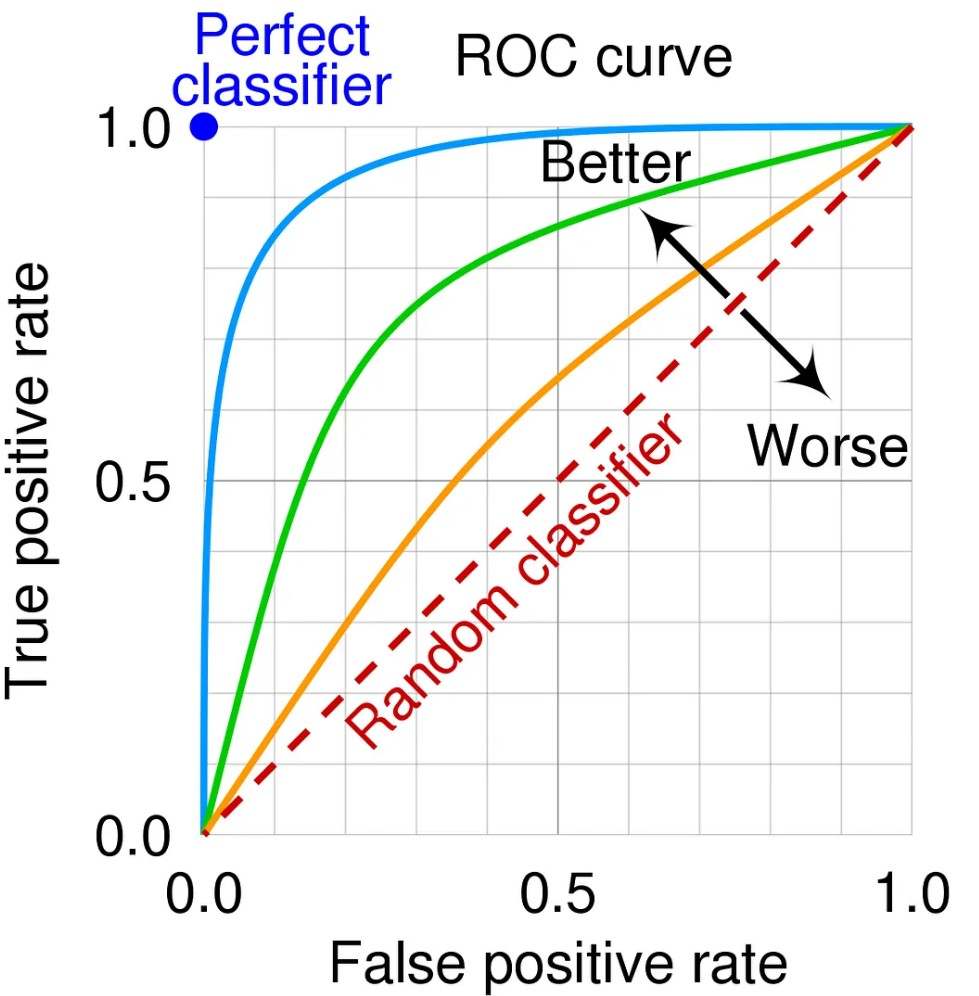
ROC曲线所围的面积称为AUC(Area Under Curve)。AUC值越大,说明分类器效果越好。
对于一个二分类器,可以取其ROC曲线最左上角的点对应的阈值为该分类器的阈值,该点一般称为CUT-OFF点。一般就是所有数据点中,TPR/FPR(或者TPR-FPR)最大的那个数据点。
3.3 回归问题(Regression)
在机器学习中,回归是一个预测性的建模任务,其目标是根据给定的一组输入变量(特征)预测一个连续的目标变量(也称为因变量)。
回归模型通常用于预测一个具体的数值或连续的结果,而不是对数据进行分类。例如:
- 回归模型可以用于预测连续的输出变量,如房价、股票价格、温度等。
- 回归模型也可以用于预测非连续的输出变量,例如点击率、转化率等,这时通常会结合一些特定的损失函数(例如二元交叉熵)来进行优化。
3.3.1 回归问题的划分
- 回归问题按照输入变量的个数,可分为一元回归和多元回归;
- 回归问题按照输入变量和输出变量之间关系的类型,可分为线性回归和非线性回归,对应的模型可分为线性模型和非线性模型。
3.3.2 机器学习中常见的回归任务
- 线性回归
- 多项式回归
- 岭回归
- Lasso回归
- ……
3.3.3 回归问题的评价指标
回归问题常用的评价指标有:
- 平均绝对误差(Mean Absolute Error, MAE):
- 均方误差(Mean Squared Error, MSE):
- 均方根误差(Root Mean Squared Error, RMSE):



