4-线性模型--(上)

4 线性模型—(上)
之前讲过,如果因变量可以被表示为自变量的线性组合,就能够用线性模型来拟合。线性关系算是日常生活中最常见的关系,比如身高和体重之间,收入和存款之间,年龄和身高之间,等等。所以可从线性模型入手,来学习机器学习。
4.1 线性回归(Linear Regression)
4.1.1 线性回归模型的引入
上一章已经介绍了回归任务,目标是预测连续型的数值目标,比如温度、价格等等。而线性回归,就是希望用线性模型,来拟合因变量为连续值的数据,如:儿童的年龄与身高之间的关系、外卖商家的到家的距离和送餐所需时间之间的关系、出租车收费与行驶路程之间的关系…
我们这里给出一个范例,【外卖配送时间和商家距离】的示例数据:
距离:1.0, 0.0, 2.0, 2.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 9.0, 10.0, 13.0, 14.0, 13.0, 15.0, 16.0, 17.0, 18.0, 18.0, 21.0, 21.0, 21.0, 24.0, 25.0, 24.0, 25.0, 26.0, 27.0, 30.0
时间:20.0, 6.0, 19.0, 25.0, 29.0, 25.0, 33.0, 41.0, 44.0, 44.0, 40.0, 35.0, 52.0, 55.0, 42.0, 53.0, 56.0, 61.0, 67.0, 67.0, 74.0, 71.0, 69.0, 85.0, 90.0, 86.0, 88.0, 86.0, 101.0, 98.0
可以画出其散点图:import matplotlib.pyplot as plt
dis = [1.0, 0.0, 2.0, 2.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 9.0, 10.0, 13.0, 14.0, 13.0, 15.0, 16.0, 17.0, 18.0, 18.0, 21.0, 21.0, 21.0, 24.0, 25.0, 24.0, 25.0, 26.0, 27.0, 30.0]
t = [20.0, 6.0, 19.0, 25.0, 29.0, 25.0, 33.0, 41.0, 44.0, 44.0, 40.0, 35.0, 52.0, 55.0, 42.0, 53.0, 56.0, 61.0, 67.0, 67.0, 74.0, 71.0, 69.0, 85.0, 90.0, 86.0, 88.0, 86.0, 101.0, 98.0]
plt.figure(figsize=(4, 3))
plt.plot(dis,t,'bo')
plt.xlabel('distance/ Km')
plt.ylabel('time / min')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title('外卖配送时间与商家距离的关系')
plt.show()
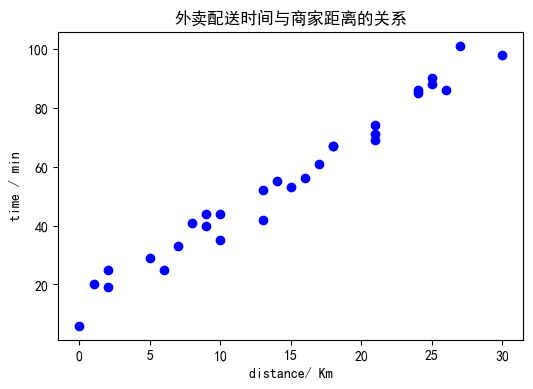
可以看到,二者的关系近似线性,我们可以尝试用一个如下的线性模型来刻画这样一种线性关系:
其中:
- $x$ 是输入数据,也称为输入样本;
- $h_w(x)$ 是预测值,也称为输出样本,有时也用 $y$ 表示;
- $w$ 和 $b$ 是模型参数;
$w$ 一般被称为权重(weight)或者系数(coefficient),$b$ 一般被称为偏置(bias)或者截距(intercept)。
关于输入数据 $x$:
- $x$ 可以是一个实数,比如在本示例中, $x$ 就代表距离,是一个实数。
- $x$ 也可以是一个多维向量(机器学习中说到向量一般都默认为列向量): 其中下标代表的是 $x$ 的维度。这代表着还有其他维度的因素会影响到回归值,比如在实际生活中,除了距离,还有天气、路况、配送时段等等因素,也可能会影响到外卖的配送时间。
- 如果 $x$ 是一个向量,那对应的权重 $w$ 就也为向量: 此时有 此时被称为多元线性回归。
对于多元线性回归,我们对于输入变量 $x$ 增设一个维度 $x_0 = 1$,去与截距 $b$ 相乘,并令 $b=w_0$,即 $\vec{x}=\{ 1, x_1, x_2, \cdots, x_n\}^T$,$\vec{w} = \{b, w_1, w_2, \cdots ,w_n\}^T$,这样就能将式(4-1-1)和(4-1-2) 统一为如下形式:
线性回归最终的目标就是希望能够学习到最合适的 $w$ 参数,来刻画 $y$ 和 $x$ 之间的线性关系。如果是二维空间的情况,就是希望找到一条直线,使得二维空间中的点,都尽可能的靠近这条直线。
回忆统计学习三要素:模型、策略、算法。至此,我们确定了线性回归问题三要素中的模型空间(假设空间)$h_w(x)$。
4.1.2 最小二乘法
最小二乘法(Least Squares Method,简写为 LS,所以也叫最小平方算法),是一种数学优化建模方法。它通过最小化误差的平方和 来寻找数据的最佳函数匹配。利用最小二乘法可以简便的求得未知的数据,并使得预测的数据与实际数据之间误差的平方和为最小。
依据最小二乘法的策略,就可以使用 平方损失 ( Residual Sum of Squares,RSS) 作为模型的损失函数,(有时候也被叫做最小二乘损失函数:Least Square Error):
上式中的右上标 $i$ 指的是第 $i$ 个输入数据,$m$ 代表训练数据的规模,即总共有多少个输入样本。
下图截取自 Wikipedia:

当所有输入数据预测值与真实值的残差是线性相关的时候,称为普通最小二乘(ordinary least squares, OLS),维基百科截图如下。


这里,我们就确定了线性回归问题的三要素中的策略:最小二乘法。
4.1.3 求解正规方程组
当面对普通最小二乘问题时,我们采用线性代数的方法,对参数值进行直接求解估算。这里用到的就是:正规方程组 Normal Equations。
首先,将 $m$ 个输入数据 $x$ 合在一起用矩阵 $X$ 表达, 并且将对应的 $m$ 个标签 $y$ 值合在一起用向量 $\vec{y}$ 表示:
注意,$ \vec{x}^{(i)} $ 本身是列向量,所以 $ (\vec{x}^{(i)})^T $ 是行向量。
$w$ 仍为: $\vec{w} = \{w_0, w_1, w_2, \cdots ,w_n\}^T$
损失函数(4-3)就可以写为:
当式(4-4-2)的损失函数最小的时候,$ \vec{w} $ 就是最优的参数值。那么令损失函数的导数 $\frac{\partial J(\vec{w})}{\partial \vec{w}}=0 $ 时,损失函数就能取得极值,此时:
得 :
式(4-4-4)就被称为正规方程组。之所以要这么变换,是因为 $ (X^T X)$一定是方阵,要求逆矩阵,必要条件是方阵。
$ (X^T X)$ 被称为正规矩阵(normal matrix)或者格拉姆矩阵(Gram matrix)。如果 $X$ 中的行向量彼此线性独立,能够推出格拉姆矩阵行列式不为0,即存在逆矩阵。 即训练样本彼此线性独立的话,(不存在多重共线性),其特征向量构成的格拉姆矩阵就是可逆的。
等式两边同时左乘以 $ (X^T X)$ 的逆 $ (X X^T)^{-1} $ 得:
至此,机器学习三要素中的最后一个算法也确定了,用正规方程组求解参数。
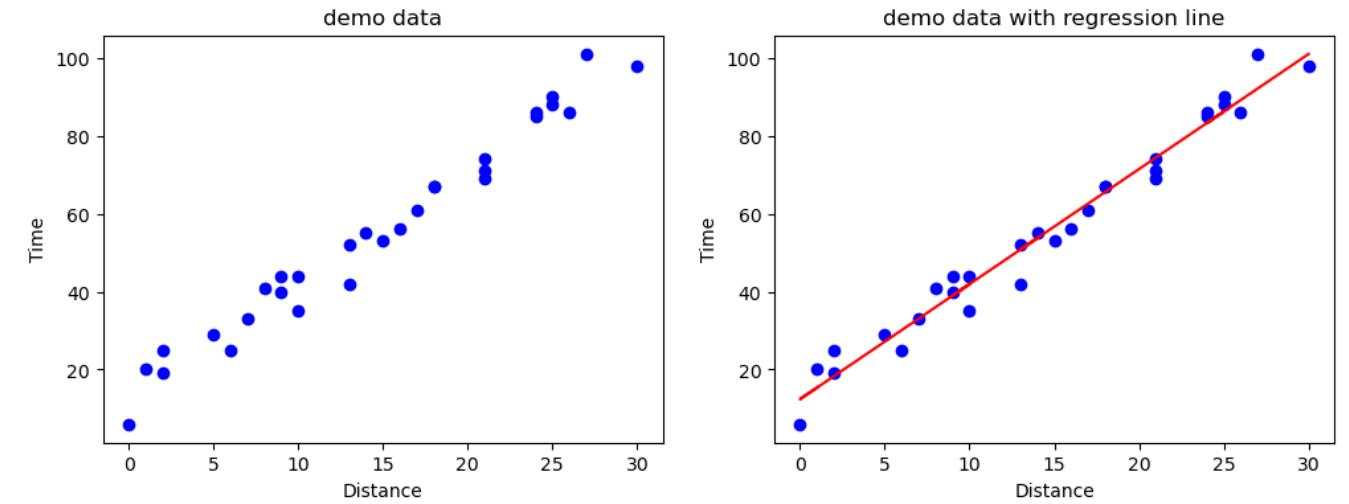
使用线性回归模型对示例数据进行拟合后,结果如下图所示:
4.1.4 最小均方算法
4.1.4.1 最小均方算法的定义
最小均方算法(Least Mean Square,简称为LMS)在互联网上经常和 最小平方算法(即最小二乘法,Least Square,简称为LS)混为一谈,其实它们是两个不同的算法,但是确实又在某些方面很相似,极容易混淆。所以这里补充讲解一下,简单的来说一下二者的联系和区别。
首先要明确的一点,是LMS方法和LS方法都是属于机器学习三要素中的策略这一部分,即依据怎样的准则选择最优的参数。
最小均方算法的起源是1960年代,由Widrow和Hoff在自适应滤波器领域提出的一种优化算法1,他们希望找到一种可以自动调整权重以最小化输出误差的方法。他们提出的最小均方滤波器(Least Mean Square Filter)如下所示:
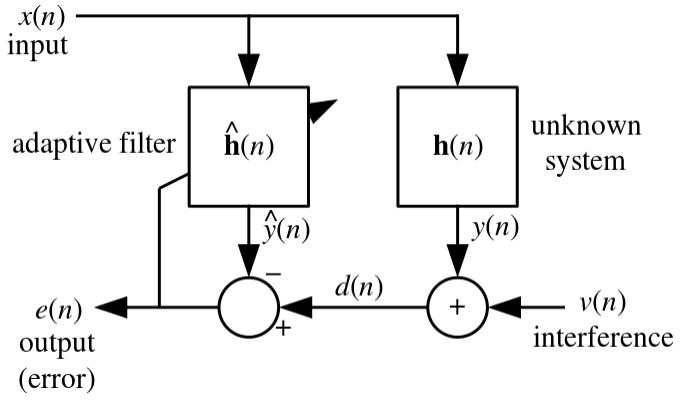
图中变量说明:
- $ x(n)$ 是输入信号脉冲
- $ h(n)$ 一个未知的滤波系统(就是待求解的滤波器)
- $ y(n)$ 是未知滤波系统的输出信号脉冲
- $ v(n)$ 是噪音
- $ d(n) = y(n) + v(n) $
- $ \hat{h}(n)$ 是自适应滤波器(目的就是期望通过这个自适应滤波器来模拟待求解滤波器
- $ \hat{y}(n)$ 是自适应滤波器的输出
- $ e(n) = d(n) - \hat{y}(n)$ 两个滤波器的输出差异
以机器学习的角度来看,$ x(n) $ 就是输入样本,$ y(n) $ 就是输入对应的真实标签(label); 现在希望能够构建一个模型 $ \hat{h}(n) $ 来拟合这个真实的未知系统 $ h(n) $,然后 $ \hat{y}(n) $ 就是模型的预测输出。
而学习的策略就是使得对于每一个输入信号脉冲 $ x(n) $,预测输出脉冲 $ \hat{y}(n) $ 与 真实系统输出脉冲 $ y(n) $ 的误差平方值最小。
而显然,仅仅输入一次信号,是无法准确的拟合一个未知滤波系统,所以需要多次输入信号,然后不断调整自适应滤波器的参数,使得输出的误差平方值最小。
所以,如果对于这个系统,后续每一次的输入信号,都使得这一次输出的误差平方值最小,就说明自适应滤波器 $ \hat{h}(n) $ 已经能够较好的拟合未知系统 $ h(n) $ 了。这就是最小均方算法(Least Mean Square)。
从这里就能知道,最小均方算法 (Least Mean Square) 中的 均本来指的是期望,而不是简单的算术平均值。
- 图一:LMS filter 定义(from Wikipedia)

- 图二:Expected Value定义(from Wikipedia)
在统计学中,期望(Expected Value)有时候也会被称为均值(Mean)。
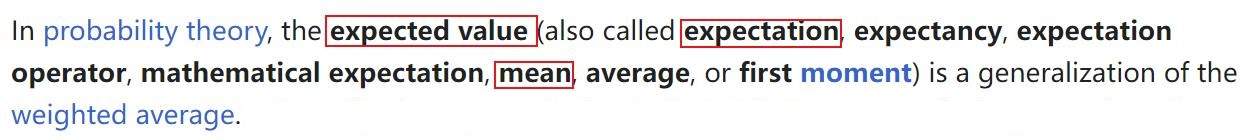
从现实情况入手分析,因为输入脉冲信号是一个接一个出现并通过滤波器的,在输入信号到来之前,是不知道该输入信号具体的情况的!所以只能通过一次又一次的迭代调整参数,最小化期望平均误差。 即希望 预测输出信号与滤波器实际输出 之差 的平方值,每一次都达到最小,从统计学的角度来看,就是误差平方变量 $ |e(n)|^2 $ 的期望值越小越好。
4.1.4.2 随机梯度下降(Stochastic Gradient Descent)
对于LMS优化算法,其每一次都只处理一个样本,所以损失函数在对于一个具体的样本而言,形式为:
即计算当前预测输出和标签的差值的平方,之所以在前方多了一个 $\frac{1}{2}$ 是为了后续求导时方便计算,这里多乘一个常量系数,只会缩放损失值的幅度,是不会对模型参数的优化结果产生影响的。
对于这个损失函数,如何来选择参数 $ w $ 来使得损失函数值最小呢?
在高等数学的微积分中我们已经学过:函数在一点沿梯度方向的变化率最大,最大值为该梯度的模。也就是说,顺着梯度方向,函数值增加的最快;逆着梯度方向,函数值减小的最快。
如图所示,假设我们从一个山坡的顶部想要下降到山底,那么根本不需要四处去试探,只需要沿着山体的最陡峭的方向往下走,我们下降的速度是最快的。而对于函数而言,其梯度方向就是陡的方向。
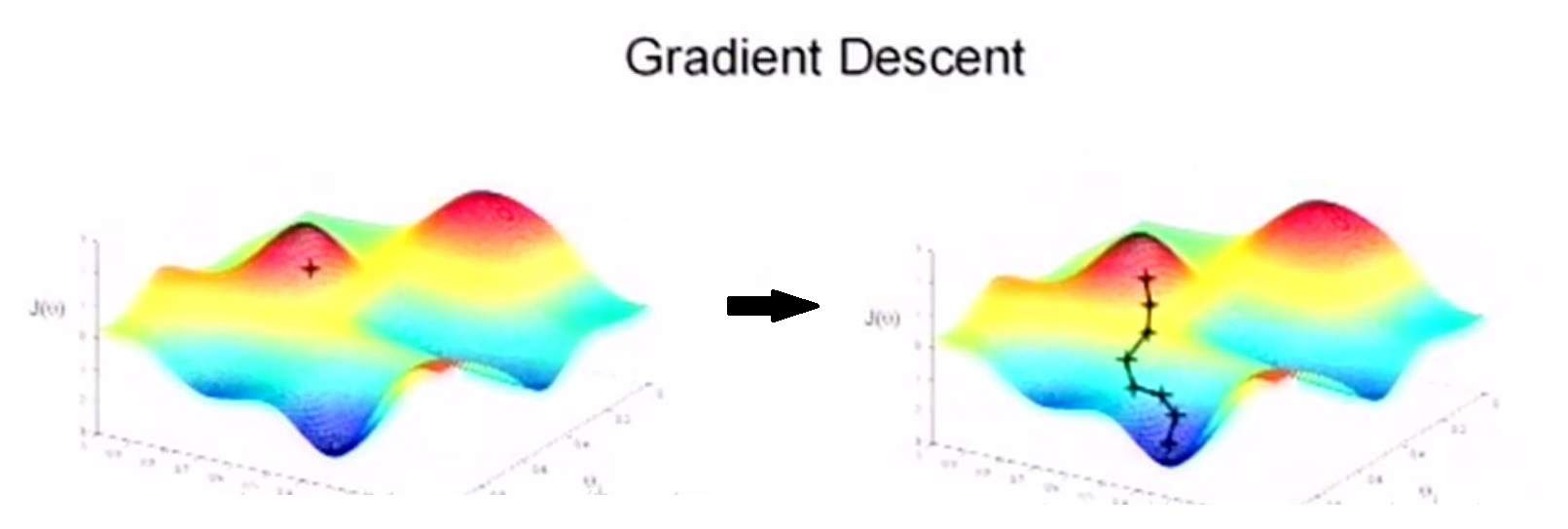
只要将参数 $ w $ 沿着负梯度方向进行更新,即每一次使得 $ w $ 向损失函数负梯度方向变化一小点,那么损失函数值也就能一点一点的变小,最终到达一个局部极小值。
这个局部极小值可能并不是全局最小值,如下图所示另一个局部极小值情况。但是基本上也是一个很小的值了,这一点就不是本节要探讨的问题了。
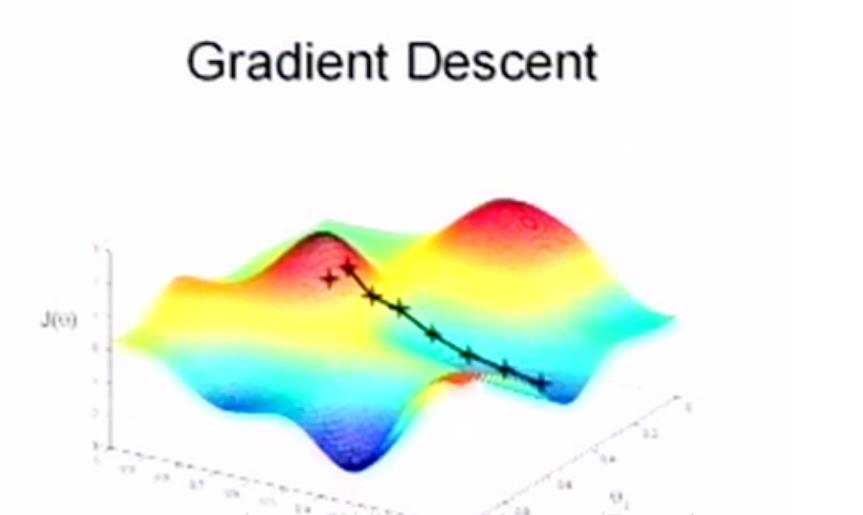
这种优化参数的算法,被称为梯度下降算法(Gradient Descent),附录中有对其更为详细的描述:梯度下降算法 。
如果每一次更新参数时,只考虑一个样本,就被更具体的称为随机梯度下降算法(Stochastic Gradient Descent)。而LMS算法(策略),其参数优化算法就是采用的随机梯度下降算法(SGD),具体操作如下:
先对损失函数求导
其中 $x_j^{(i)}$ 为第 $i$ 个样本的第 $j$ 个特征值, $y^{(i)}$ 表示第 $i$ 个样本的标签值。
另外,LMS自适应滤波器是一个线性滤波器,所以可以用上面提到的线性模型 $h_w(\vec{x}^{(i)}) = \vec{w}^T\vec{x}^{(i)}$ 表示。
所以对于参数 $\vec{w} = \{w_1, w_2, \cdots , w_j ,\cdots, w_n\}^T$ 而言,其各个维度 $w_j$ 具体的梯度分量表达式就为:
所以,每一次对于该权重参数分量 $ w_j $ 的更新公式就为:
其中 $\alpha$ 为学习率,是一个超参数,控制每一次迭代更新参数的一个幅度;也就是理解为下坡的时候,一步跨多远的距离,所以也被称为“步长”。 学习率过小的话,则需要迭代很多次才能收敛,学习率过大,则可能出现震荡,甚至发散。
总结起来,最小均方算法(LMS)就是利用随机梯度下降(SGD)算法,每次都利用当前一个样本的数据,来更新参数。
4.1.5 最小均方算法(LMS)和最小平方算法(LS)的联系
从机器学习三要素(模型、策略、算法)这三个角度来分析LS和LMS算法的异同点:
- 模型
LS和LMS都是可以用来拟合线性模型的,在解决线性回归问题时,假设空间都可以表示为 策略
二者的损失函数都要计算残差平方:- LS 算法用的是平方误差(Residual Sum of Squares, RSS):是对于所有训练样本而言,每个样本对应的预测输出值与标签的误差的平方的总和 最小,是典型的离线学习:将所有的数据收集齐后,再进行一次性训练。
LMS 算法用的是均方误差(Mean Squared Error, MSE):
维基百科中对 均方误差(MSE) 的定义:

重点看一下这两句话:
“MSE is a risk function, corresponding to the expected value of the squared error loss.”
MSE是一个风险函数,对应于误差损失平方的期望值。“In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).”
在机器学习中,特别是经验风险最小化,MSE可以将经验风险(观察数据集上的平均损失)作为真MSE(真风险:实际总体分布上的平均损失)的估计。也就是说,均方误差(MSE)的原始定义就是:误差的平方的期望值。 事实上,维基百科对于该词条的中文介绍也写明了,只不过中文介绍一般内容比较简略,所以我通常直接引用的是如上的英文版。

但是,期望值一般都是一个统计学上的概念,它是想表达对于任何的输入而言的一种统计考量,但是实际的训练数据是有限的,所以一般也可以用基于整个训练集的误差平方和的算数平均值来近似代替。
所以在很多地方通常都能看到用如下表达式来表示均方误差(MSE):即平方误差(式4-11)的基础上多了一个求平均 $\frac{1}{m}$ 而已。但是一定要注意,这只是在确定能够全部获得m个样本的情况下才能用。
Wikipedia也有这种表述情况:
它称其为样本内均方误差(within-sample MSE)。
所以当训练集的样本是有限的、且确定、且样本规模足够大(辛钦大数定律)的情况下,均方误差(MSE)的确实可以写成式(4-12-2)的形式。
辛钦大数定律,当样本个数足够大时,样本 $(X_1, X_2, \cdots, X_n)$ 的算术平均值依概率收敛于总体数学期望$ E(X)$
如果是在线学习(online learning)的情况下,则一般用如下形式来表示均方误差:即一次只能得到一个样本的情况。
另外还有一个不容易注意到的点,那就是英文中的 mean 一词,它既可以表示 算术平均值(Arithmetic_Mean) ,也可以表示总体均值 or 期望(Population mean or Expected value), 所以这也是很多中文机器学习书籍中容易引起混淆的原因。
总结:依据最小均方算法(LMS)的起源,均方误差(MSE)原始定义是误差的平方的期望值,在机器学习里,通常用样本内均方误差(within-sample MSE)或者说误差平方和的平均值来近似代替该期望值,但是这要求训练样本集的规模足够大。
- LS 算法用的是平方误差(Residual Sum of Squares, RSS):是对于所有训练样本而言,每个样本对应的预测输出值与标签的误差的平方的总和 最小,是典型的离线学习:将所有的数据收集齐后,再进行一次性训练。
- 算法
- LS算法后续一般通过解正规方程组来求解参数。
- LMS算法后续一般通过随机梯度下降来求解参数。
- 总结
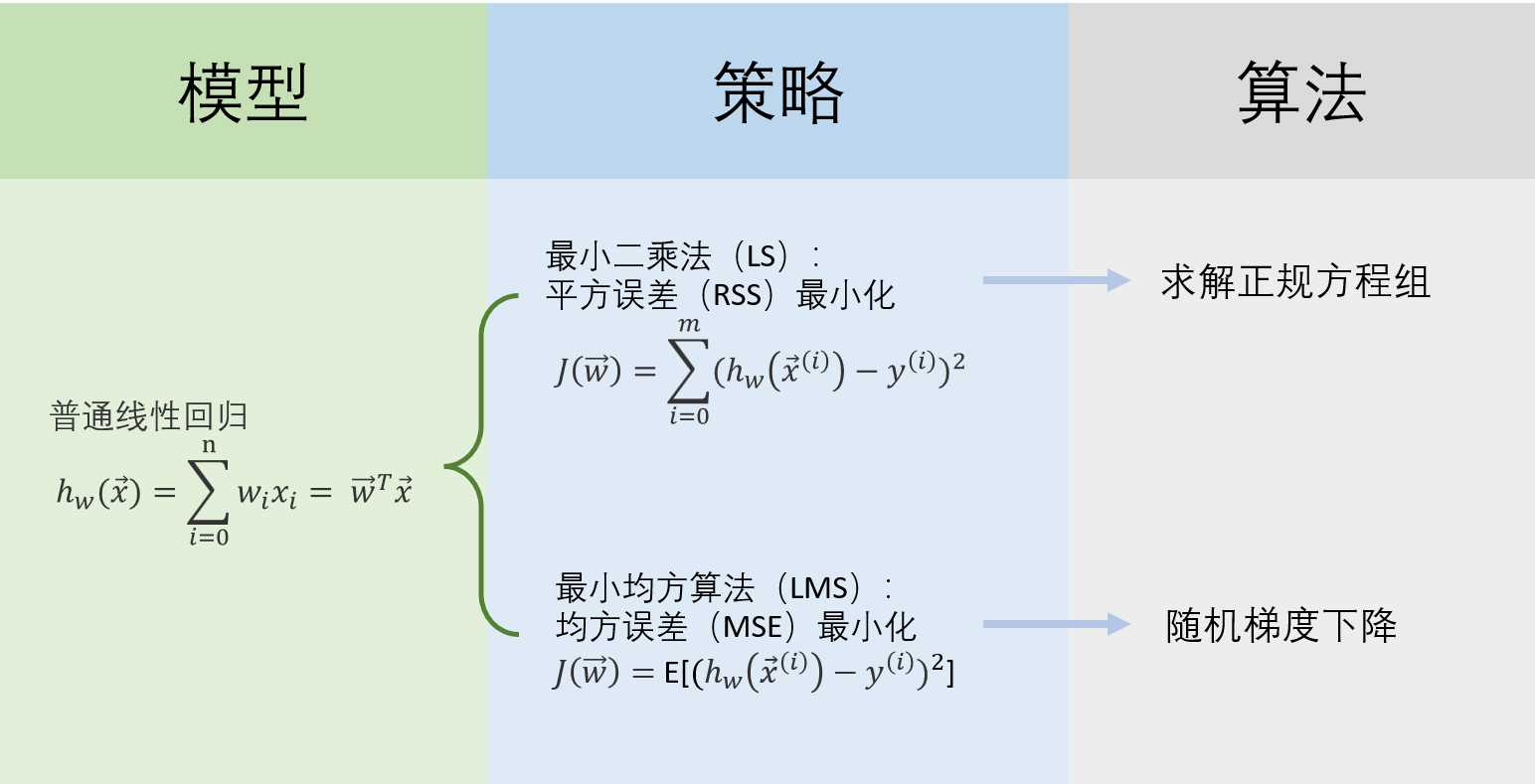
本文其余参考资料2
1:Widrow, B., & Hoff, M. (1960, August). Adaptive switching circuits. In 1960 IRE WESCON Convention Record, Part 4, pages 96-104. New York: Institute of Radio Engineers.
2:Andrew Ng. (n.d.). CS229: Machine Learning. (Lecture notes Chapter 1). Stanford University.



