5 感知机

5.1 感知机模型

感知机(perceptron)是一种用于二分类的线性分类模型：输入为实例的特征向量，输出为实例的类别，取+1和-1二值。

感知机是1957¹年提出的，比较早的一个模型，但是它算是SVM和神经网络模型的基础。如果之前已经了解过逻辑回归(logistic regression)，其实就比较容易理解感知机了，硬要说的话，逻辑回归其实是从感知机发展而来的。

感知机模型可以用下面的公式来表示：

$f(x) = sign(w \cdot x + b) \tag {5-1}$

其中，$w \cdot x + b$ 是线性方程，$w$是权值(weight)，$b$是偏置(bias)，$sign$是符号函数。
符号函数的定义如下：

$sign(x) = \begin{cases} +1, & x \ge 0 \\ -1, & x < 0 \end{cases} \tag {5-2}$

其图像示例为：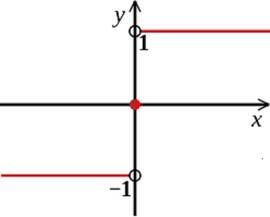

即，符号函数对大于等于0的值，映射为1；对小于等于0的值，映射为-1。

对于线性部分 $w \cdot x + b$ 的结果施加的函数，可以称为激活函数(activation function)。所以，当激活函数为 $sign$ 函数时，模型就是感知机；激活函数为 $sigmoid$ 函数时，模型就成了逻辑回归。二者的图像画在一起如下：

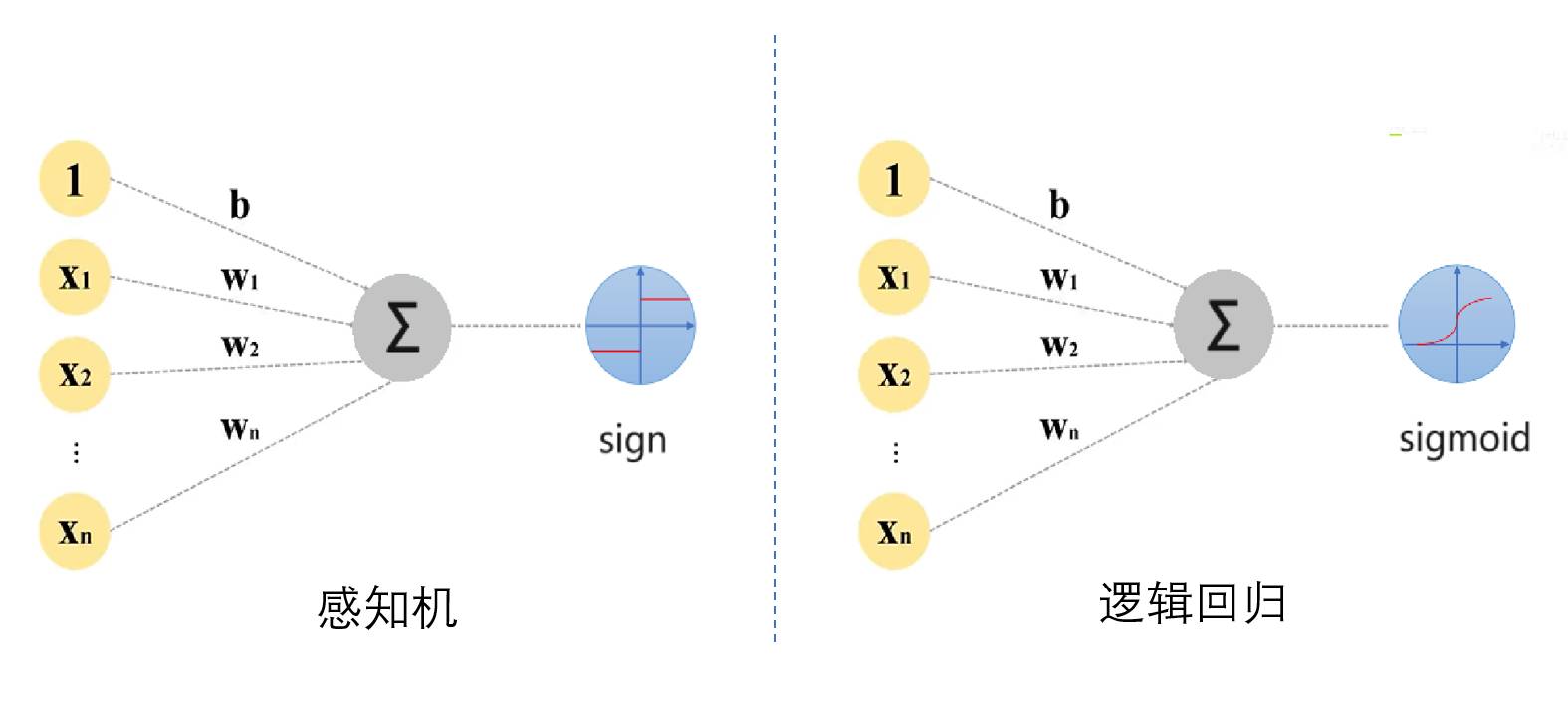
可知，感知机的结果就是1或者-1，而逻辑回归的结果是0到1之间的连续值，所以逻辑回归依然用的是“回归”名字，只不过可以通过取阈值 threshold 来做进一步的二分类。

在深度学习领域，还有更多的激活函数，比如 ReLU、Leaky ReLU、ELU 等，这里不做赘述。

一个线性加权和经过激活函数，这样的结构被称为 M-P 神经元，它是 1943 年Minsky 和 Papert² 模拟神经元的工作原理而提出的。

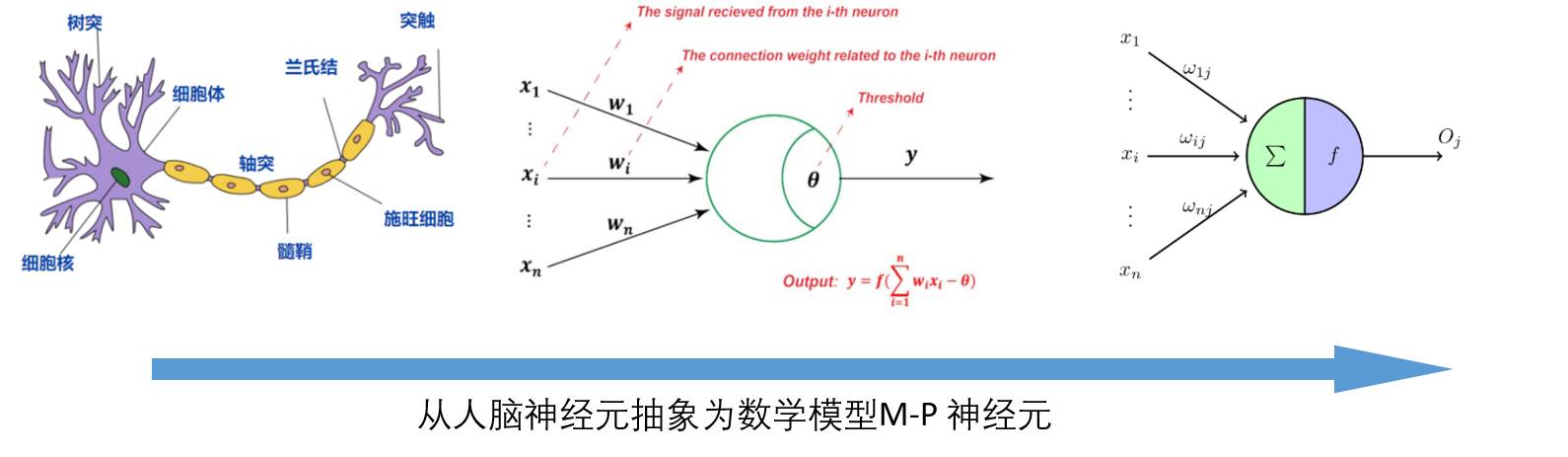
5.1.1 感知机的目的

感知机模型的目的，就是找到一个最优的分类边界，使得分类结果尽可能的好。也就是说，最终目标就是使得 $w \cdot x + b=0$ 形成的线性超平面（二维的情况就是一根线，三维的情况就是一个面，多维的情况就是超平面），能够将样本分割为正、负两部分，如下图所示。

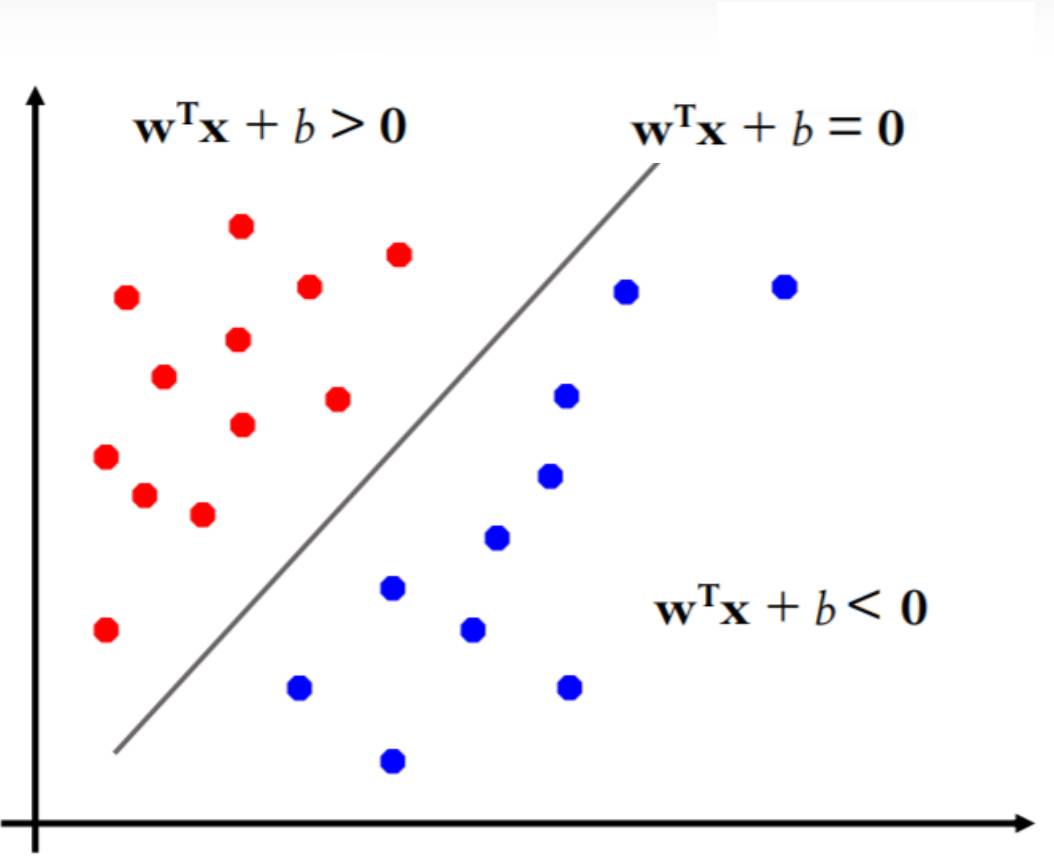
如果一个数据集能够找到至少一个超平面将样本点正确地分割开，就称该数据集为线性可分的。如果一个数据集无法找到一个超平面将其分割开，就称该数据集为线性不可分的。

5.1.2 感知机的学习策略

上面提到，感知机就是期望找到一个线性超平面将数据集分为两部分，所以要确定超平面 $w \cdot x + b=0$ 就是要确定其法向量 $w$ 和截距 $b$ 这两个参数，所以就需要确定一个损失函数，并将损失函数极小化来获取对 $w$ 和 $b$ 的估计。

损失函数的一种想法是，统计误分类点的个数，然后用误分类点的个数来作为损失函数。但是，这样的损失函数不是参数 $w$ 和 $b$ 的连续可导函数，所以无法使用梯度下降法来求解。

另一种想法是，统计误分类点到超平面的距离，来作为损失函数。这样，损失函数就是参数 $w$ 和 $b$ 的连续可导函数，就可以使用梯度下降法来求解。

点 $x_0$ 到平面的距离公式为：

$\frac{1}{||w||} |w \cdot x_0 + b| \tag{5-3}$

其中，$||w||$ 表示法向量 $w$ 的模，也就是 L2 范数。

对于误分类点 $(x_i, y_i)$ ，有两种情况：

点 $x_i$ 在超平面的左侧，即 $w \cdot x_0 + b < 0$ ，分类结果为-1，但标签却为 $y_i=1$ ，那么点 $x_i$ 到超平面的距离为： $\frac{1}{||w||} |w \cdot x_0 + b| = \frac{1}{||w||} \cdot -y_i(w \cdot x_0 + b) \tag{5-4-1}$
点 $x_i$ 在超平面的右侧，即 $w \cdot x_0 + b > 0$ ，分类结果为 1，但标签却为 $y_i=-1$ ，那么点 $x_i$ 到超平面的距离为： $\frac{1}{||w||} |w \cdot x_0 + b| = \frac{1}{||w||} \cdot -y_i(w \cdot x_0 + b) \tag{5-4-2}$

所以会发现，误分类点到超平面的距离，去掉绝对值符号后都可以统一写为：

$\frac{1}{||w||} \cdot -y_i(w \cdot x_0 + b) \tag{5-4-3}$

则假设误分类点的集合为 M，则损失函数为：

$L(w, b) = -\frac{1}{||w||} \sum_{x_i \in M}{y_i(w \cdot x_i + b)} \tag{5-5-1}$

对于感知机来说，损失函数可以不考虑 $||w||$ 部分，直接将损失函数写为：

$L(w, b) = - \sum_{x_i \in M}{y_i(w \cdot x_i + b)} \tag{5-5-2}$

思考的角度不是说直接去掉 $||w||$ 部分，而是假设 $||w||$ = 1。 因为任何一个超平面都可以将其改写为 $||w||$ = 1 的形式，即对每个系数都除以 $||w||$ 即可，同时超平面本身不会变化。比如对于一个超平面：

$3\cdot x_1 + 4 \cdot x_2 + b = 0 \tag{5-6-1}$

将其改写为:

$\frac{3}{5} \cdot x_1 + \frac{4}{5} \cdot x_2 + \frac{b}{5} = 0$

其实超平面还是原来那个超平面，但是改写后的 $||w||$ = 1 。

5.1.3 参数优化算法方法

采用随机梯度下降(SGD)的方法，对损失函数求梯度：

$\begin{aligned} \nabla_wL(w,b) & = -\sum_{x_i \in M}{y_ix_i} \\ \nabla_bL(w,b) & = -\sum_{x_i \in M}{y_i} \\ \end{aligned} \tag{5-7}$

则更新公式为：

$\begin{aligned} w & := w - \eta \cdot \nabla_wL(w,b) \\ b & := b - \eta \cdot \nabla_bL(w,b) \\ \end{aligned} \tag{5-8}$

其中 $\eta$ 为学习率。每一次选取一个误分类点即可。这样通过不断迭代就能使得损失函数 $L(w, b)$ 不断减小，直到为0，就说明没有误分类点了。

5.1.4 算法收敛性

根据 Novikoff定律，当训练集数据线性可分时，感知机算法是收敛的。如果训练集数据线性不可分，则感知机算法不收敛，迭代结果发生震荡。

需要注意的是，感知机学习算法对训练数据集的元素顺序敏感，即误分类点选取的顺序不同，可能导致学习结果的不同。同时，感知机算法对于参数初始值也比较敏感，如果初始值设置不当，可能会导致学习失败。

5.2 多层感知机

5.2.1 感知机的局限性

感知机的局限性：感知机不能解决异或问题。

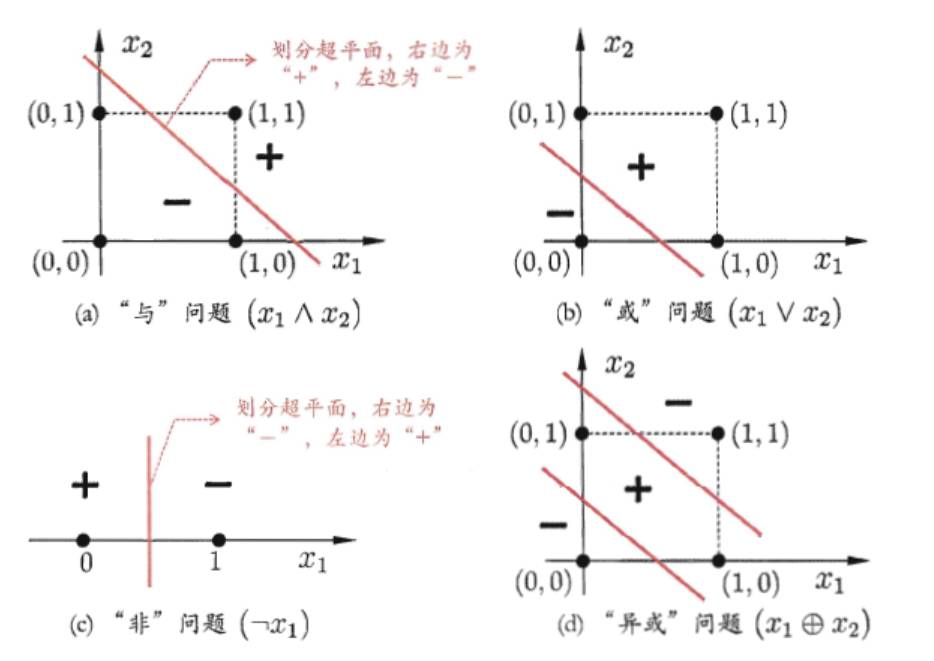
如果所示，用一个超平面是无法将异或问题划分的，它是属于线性不可分问题，一般有两个思路：

对输入数据做处理，看看能否将输入数据映射到高维度空间中，在高维空间或许能找到一个线性超平面，将其分开。这其实就是 SVM 算法中的核方法。
用多个感知机，每个感知机负责将一部分数据分开，最后将分开的数据合并起来。这其实就是多层感知机。

多层感知机能解决异或问题：

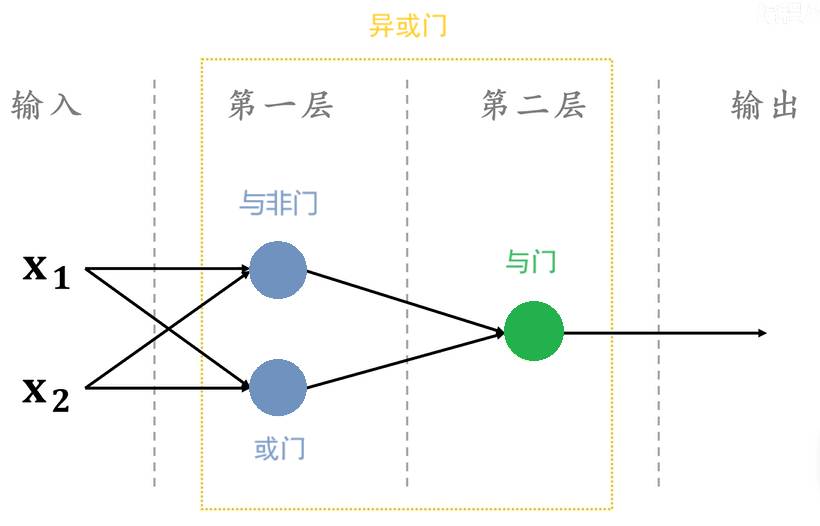
如果所示的多层神经网络，第一层用了两个神经元，一个神经元用来实现与非门，一个神经元用来实现或门；第二层用了一个神经元，用来实现与门。最终整个多层感知机，实现了异或门的功能。

5.2.2 多层感知机的发展

由于多层感知机可以解决异或问题的启发，可以想到，如果增加神经元的层数，是可以解决更复杂的问题的。
如图所示：

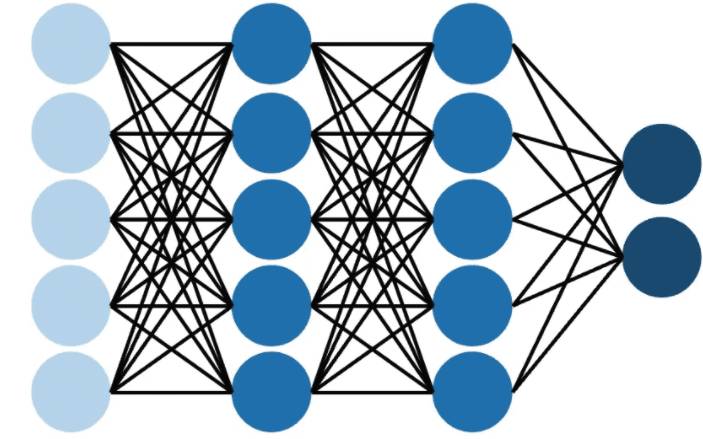
多层感知机中，每一个神经元的输出，都输入到下一层所有的神经元中；除第一层外，每个神经元的输入都是上一层所有神经元的输出，按照现在深度学习的叫法，这种连接方式称之为“全连接(Fully-Connected)”，从数学角度看就是在做矩阵乘法。

Hornik 等人在1989³年证明，只要多层感知机中的神经元个数和层数足够多，那么多层感知机就能以任意精度逼近任何连续函数，足见其强大的表示能力。同时，BP(反向传播)算法的提出，使得多层感知机能够以较简单的方式训练。到现在，得益于计算力和数据的飞速爆炸，脱胎于多层感知机的深度学习，已经成了人工智能领域的主流技术。

目前神经网络和深度学习已然成为了一门单独的学科，但是它的发展历程和理论基础，都和多层感知机有着千丝万缕的关系。所以深度学习其实可以被看作是多层感知机的一个延伸和扩展，是机器学习算法的一个分支。

¹:Frank Rosenblatt. (1957). The perceptron: A perceiving and recognizing automaton. Report 85-460-1. Cornell Aeronautical Laboratory.
²:McCulloch, W. S., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5, 115-133.
³:Hornik, K., Stinchcombe, M., & White, H. (1989). Multilayer feedforward networks are universal approximators. Neural networks, 2(5), 359-366.