---

4 线性模型—(下)

---

4.5 逻辑回归(Logistic Regression)

逻辑回归(Logistic Regression) 也被称为对数几率回归（Logit Regression），它是在线性回归的基础之上做了改进，输出值依然是连续值，所以称“回归(Regression)”。虽然名字依然是回归，但它主要是用来处理二分类问题的。

这是因为它的输出值依然是连续值，但是它是将线性回归的输出结果通过Sigmoid函数转换为0~1之间的概率值，然后通过概率值来判断分类。

至于为何 Sigmoid 函数的输出值能够视为概率值，是可以通过广义线性模型(GLM) 和 指数分布族推导出来的，后面有介绍。

4.5.1 Logistic Function

Logstic Function，也被称为 Sigmoid Function，它的公式如下:

$$g(z) = \frac{1}{1+e^{-z}} \tag{4-22}$$

它的图像如下:

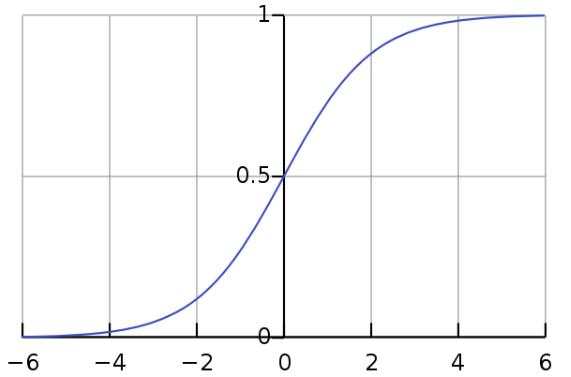
由图像可知，Sigmoid 函数可以将一个实数映射到(0,1)的区间。

Sigmoid函数的导数有一个很好的性质：

$$\begin{aligned} g'(z) &= \frac{d}{dz} (\frac{1}{1+e^{-z}} )\\ &= \frac{1}{(1+e^{-z})^2} \cdot (-e^{-z}) \\ &= \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}} \\ &= \frac{1}{1+e^{-z}} \cdot (1-\frac{1}{1+e^{-z}} )\\ &= g(z) \cdot (1-g(z)) \end{aligned}$$

即 $g'(z) = g(z) \cdot (1-g(z)) \tag{4-23}$

4.5.2 逻辑回归的预测函数

我们知道，线性回归的预测函数可以表示为：

$$\hat{y} = h_w(x)= \vec{w} \vec{x}+b \tag{4-24}$$

此时预测值 $y$ 的值域范围是 $ (-\infty,+\infty) $，如果我们再在此基础之上，外套一个Logistic(Sigmoid)函数，那么此时的预测函数的值域范围就变成了 $(0,1) $ ，即：

$$\hat{y} = g( h_w(x)) = g(\vec{w} \vec{x}+b)= \frac{1}{1+e^{-\vec{w} \vec{x}+b}} \tag{4-25}$$

这就是 Logistic Regression 名字的由来！

如果将该预测函数运用于二分类问题，那么 $\hat{y}$ 就可以用来代表样本 $x$ 属于正例的概率值，则 $1-\hat{y}$ 就可以用来代表样本 $x$ 属于负例的概率值。那么就可以自己设定一个阈值 $thresh$ (通常默认就是0.5)， $\hat{y}>thresh$ 就可以认为样本 $x$ 属于正例， $\hat{y}<thresh$ 就可以认为样本 $x$ 属于负例；由此，就能够实现二分类！

如果将上式恢复成线性回归的形式，只需要化简两边同时取 $ln$ ：

$$ln \frac{\hat{y}}{1-\hat{y}} = \vec{w} \vec{x}+b \tag{4-26}$$

若 $y$ 代表样本属于正例的概率值， $ 1-y $ 代表样本属于负例的概率值，则二者的比值在统计学中就称为几率(odds) ：

$$odds = \frac{\hat{y}}{1-\hat{y}} \tag{4-27}$$

那么对几率求对数就是对数几率(log-odds)，也作 logit，故式子可以继续改写 ：

$$\vec{w} \vec{x}+b = ln \frac{\hat{y}}{1-\hat{y}} = logit(\hat{y})\tag{4-28}$$

即逻辑回归的预测函数，可以转化为普通线性回归的形式，就可以理解为在对“对数几率(log-odds)”进行线性回归预测，预测值是 $\hat{y}$ 的对数几率值； 因此，Logistic Regression 又被称为 Logit Regression，即“对数几率回归”。

4.5.3 逻辑回归的损失函数

讨论损失函数，就是在讨论如何衡量预测值和真实值之间的差距，从而决定如何调整参数，即机器学习三要素的策略。

为了同之前讲的线性回归统一起来，假设仍使用 $h(·)$ 来表示预测函数，则逻辑回归的预测函数可以写为:

$$h_w(x) = \frac{1}{1+e^{-\vec{w}\vec{x}}} \tag{4-29}$$

逻辑回归的损失函数被称为交叉熵损失函数(Cross-Entropy Loss):

$$J(w) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \ln h_w(x^{(i)}) + (1-y^{(i)}) \ln (1-h_w(x^{(i)})) \right] \tag{4-30}$$

其中 ，$m$ 表示样本个数，$y^{(i)}$ 表示第 $i$ 个样本的真实标签，$h_w(x^{(i)})$ 表示第 $i$ 个样本的预测值。

我们可以从下面三个方向来理解这个损失函数：

1. 交叉熵(Cross Entropy)

   • 熵
     熵表示的是随机变量不确定性的度量，熵越大，随机变量的不确定性就越大。 其计算公式如下：

     $$H(X) = -\sum_{x \in X} p(x) \ln p(x) \tag{4-31}$$

     其中，$X$ 表示随机变量，$p(x)$ 表示随机变量取值为 $x$ 的概率。
     
     

   • 交叉熵
     交叉熵表示的是两个概率分布之间的距离，交叉熵越大，两个概率分布就越相似。 其计算公式如下：

     $$H(p,q) = -\sum_{x \in X} p(x) \ln q(x) \tag{4-32}$$

     在机器学习问题中，可以将 $p(x)$ 表示真实分布，$q(x)$ 表示预测分布，这样真实分布与预测分布之间的交叉熵，即能表示模型从数据中学得的概率分布 $q(x)$ 与数据的真实分布 $p(x)$ 有多接近，进而衡量模型的好坏。
     
     

1. 极大似然估计

   在上面我们提到，逻辑回归的预测值 $\hat{y}$ 是可以被视为二分类问题中样本 $x$ 属于正例的概率值，那么样本为负例的概率值就可以写为 $1-\hat{y}$。 所以将两种类别的概率表达式写出：

   $$\begin{aligned} P(y=1 |x; w) &= h_w(x) \\ P(y=0 | x; w) &= 1-h_w(x) \end{aligned} \tag {4-33}$$

   这两个情况可以整合成一个统一的式子：

   $$P(y| x; w) = \left[h_w(x) \right]^y \left[1-h_w(x)\right]^{1-y} \tag {4-34}$$

   假设 m 个样本都是相互独立的，那么写出参数 $w$ 的似然函数：

   $$L(w) = \prod_{i=1}^m P(y^{(i)}|x^{(i)}, w) = \prod_{i=1}^m \left[h_w(x^{(i)}) \right]^{y^{(i)}} \left[1-h_w(x^{(i)}) \right]^{1-y^{(i)}} \tag {4-35}$$

   关于似然函数的相关知识，属于概率论与数理统计中的一个常用且经典的知识点，这里就不展开讨论了。

   写出上式的对数似然函数：

   $$\ln L(w) = \sum_{i=1}^m y^{(i)} \ln h_w(x^{(i)}) + (1-y^{(i)}) \ln (1-h_w(x^{(i)})) \tag {4-36}$$

   极大似然估计就是希望获得参数的估计值，能够使极大似然函数值取得最大。

   所以，逻辑回归的损失函数可以写为如下所示，相当于是在似然函数前面多了负号，则该损失函数取得极小值时，对应似然函数就取到极大值：

   $$J(w) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \ln h_w(x^{(i)}) + (1-y^{(i)}) \ln (1-h_w(x^{(i)})) \right] \tag {4-37}$$

   这个其实就是交叉熵的形式，所以该损失函数被称为交叉熵损失函数。
   真实分布$p(x)$ 的取值为 $y^{(i)}$ 或者 $1-y^{(i)}$；
   预测分布$q(x)$ 的取值为 $\ln h_w(x^{(i)})$ 或者 $1- \ln h_w(x^{(i)})$。
   总结：逻辑回归的损失函数 — 交叉熵损失函数，是可以通过极大似然估计来推导出的。
   
   

2. 相对熵(relative entropy)

   相对熵也叫 KL 散度，用来衡量两个概率分布之间的相似程度。

   相对熵定义为：

   $$D_{KL}(p||q) = \sum_{x\in X} p(x) \ln \frac{p(x)}{q(x)} \tag {4-38}$$

   将以上公式进行推导：

   $$\begin{aligned} D_{KL}(p||q) &= \sum_{x\in X} p(x) \ln p(x) - \sum_{x\in X} p(x) \ln q(x) \\ &= -H(p) + H(p,q) \end{aligned} \tag {4-39}$$

   由于在当前问题中，$p$ 是真实分布（即训练样本的分布），所以其熵 $H(p)$ 是一个确定的常量，所以 $p$ 和 $q$ 之间的相对熵 $ D_{KL}(p||q) $ 其实仅取决于二者之间交叉熵 $H(p,q)$ 的大小， 所以可以用交叉熵作为损失函数来衡量 训练样本的真实分布 与 模型输出的分布之间的差异大小。

4.6 多分类逻辑回归(Multinomial Logistic Regression)

传统的逻辑回归只能解决二分类问题，如果要解决多分类问题，就需要对逻辑回归进行改造，使其能够处理多分类问题。

4.6.1 One-Vs-All(OvA)

One-Vs-All 方法是解决多分类问题的一个常用方法，也被称为 “一对多” ，也有叫它 One-vs-Rest(OVR) 的，总之是表达这么一个思路：

对于每一个类别，都单独训练一个二分类的逻辑回归分类器，这个分类器只能处理这个类别，它的功能是判断输入样本（是属于这个类别，还是不属于这个类别） 这个二分类问题。

假设现在有一个问题是要将数据分为 A、B、C、D 四个类别，那么我们可以训练四个二分类的逻辑回归分类器，每个分类器只能处理一个类别，即：

• 第一个分类器 L_a，它只判断样本是否属于 A 类别；
• 第二个分类器 L_b，它只判断样本是否属于 B 类别；
• 第三个分类器 L_c，它只判断样本是否属于 C 类别；
• 第四个分类器 L_d，它只判断样本是否属于 D 类别；

在训练时，每个训练样本都要并行的进入这四个分类器去拟合其参数；
在测试时，每个测试样本也都并行的进入这四个分类器，去获得四个不同的sigmoid输出，一般挑选输出最大的那个分类器代表的类别来作为预测类别。

总结起来，如果有N个类别，那这种 OVA 思路就要建立 N 个不同的二分类逻辑回归模型，每个模型只能处理一个类别。

4.6.2 One-Vs-One(OvO)

One-Vs-One(OvO)是指的 “一对一”，会针对类别两两组合建立二分类器，依然用分 A、B、C、D 四个类别的数据举例：

• 第一个分类器 L_a_b，它只判断样本是否属于 AB 类别；
• 第二个分类器 L_a_c，它只判断样本是否属于 AC 类别；
• 第三个分类器 L_a_d，它只判断样本是否属于 AD 类别；
• 第四个分类器 L_b_c，它只判断样本是否属于 BC 类别；
• 第五个分类器 L_b_d，它只判断样本是否属于 BD 类别；
• 第六个分类器 L_c_d，它只判断样本是否属于 CD 类别；

所以一共建立了六个二分类模型，每个模型只能处理两个类别，
在训练时，每个分类器仅仅只需要用到两种类别的训练样例；
在测试时，每个测试样本是需要并行的进入这六个分类器，每个分类器会做出一个类别预测，相当于是投票，最后投票数最多的类别就是预测类别。

总结起来，如果有N个类别，那这种 OvO 思路就要建立 N(N-1)/2 个不同的二分类逻辑回归模型，每个模型只能处理两个类别。

4.6.3 Multi-nomial

Multi-nomial 是指的 “多分类”，从宏观的角度上来看，可以理解为只建立了一个逻辑回归模型，但是要注意这个逻辑回归模型的权重参数的维度已经发生了变化。

• 二分类情况
  回顾在做二分类时，假设输入样本的特征维度是 K(假设已经将截距b考虑进去了)，可以将输入表示为一个 K 维的向量：

  $$\vec{x}= \{x_1, x_2, ..., x_k\} ^ T$$

  线性函数的参数也表示为一个 K 维向量：

  $$\vec{w }= \{w_1, w_2, ..., w_k\}^T$$

  两者的向量积 $\vec{w}^T\vec{x}$ 是一个 $1*1$ 维的实数，然后再将该实数通过Sigmoid函数做映射。

• 多分类情况
  如果是多分类，假设输入样本的特征维度是 K，则线性函数的参数可以表示为一个 $C*K$ 的矩阵，其中 $C$ 表示类别数目： $$W = \left[ \begin{matrix} w_{11} & w_{12} & ... & w_{1k} \\ w_{21} & w_{22} & ... & w_{2k} \\ ... & ... & ... & ... \\ w_{C1} & w_{C2} & ... & w_{Ck} \end{matrix} \right] \tag {4-40}$$ 所以二者相乘的结果 $ W \vec{x} $ 是一个 $C*1$ 的向量：

$$\vec{z} = \{ z_1, z_2, ..., z_C \} \tag {4-41}$$

到这里很容易就产生一个想法，只要对这个 C 维的列向量做一次处理，那是不是就能让列向量中的每个值，代表它属于各个类别的概率了呢？然后从中挑选出概率值最大的那个维度代表的类别，就可以得到预测类别的结果了。

1. Softmax function

   Softmax function 将一个含任意实数的 K 维向量 z “压缩” 到另一个 K 维实向量 σ(z) 中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。它的表达式如下：

   $$softmax(z) = \frac{e^{z_j}}{\sum_{j=1}^K e^{z_j}} \tag {4-42}$$

   那么如果对上面得到的那个向量 $\vec{z} = \{ z_1, z_2, …, z_C \} $ 做softmax处理，就可以得到一个新的向量：

   $$\vec{\hat{y}} = softmax(\vec{z}) = \{ \frac{e^{z_1}}{\sum_{j=1}^K e^{z_j}}, \frac{e^{z_2}}{\sum_{j=1}^K e^{z_j}}, ..., \frac{e^{z_C}}{\sum_{j=1}^K e^{z_j}} \} ^T \tag {4-43}$$

   向量 $\vec{\hat{y}}$ 中的每一个元素都是 0 到 1 之间的实数，并且它们的和为1，所以可以将该向量作为对于样本 $\vec{x}$ 的类别预测向量，其中的分量 $\hat{y_j}$ 表示样本 $\vec{x}$ 属于类别 j 的概率（也是可以由广义线性模型和指数分布族推导出来的）。
   
   

2. Softmax loss

   二分类逻辑回归的损失函数是使用的交叉熵损失函数，多分类的逻辑回归的损失函数也用的是交叉熵损失函数：
   假设有 K 个类别，则单样本x 的交叉熵为：

   $$H(p,q) = - \sum_{j=1}^K y_j \ln(\hat{y_j}) = - \sum_{j=1}^K y_j \ln(\frac{e^{z_j}}{\sum_{j=1}^K e^{z_j}}) \tag {4-44}$$

   $y_j$ 是真实分布 $p$ 中第 j 个类别的概率，$\hat{y_j}$ 也即 $\frac{e^{z_j}}{\sum_{j=1}^K e^{z_j}}$ 是预测分布 $q$ 中第 j 个类别的概率。

   则对于m个训练样本，多分类逻辑回归的交叉熵损失函数为：

   $$J(W) = - \frac{1}{m} \sum_{i=1}^m \sum_{j=1}^K y_{mj} \ln(\frac{e^{z_{mj}}}{\sum_{j=1}^K e^{z_{mj}}}) \tag {4-45}$$

   考虑到一个情况，那就是训练时，作为 label一般会进行 onehot 编码处理，比如若样本属于 A,B,C,D 四个分类中的 B 类，则 label 可以用如下 onehot 向量表示：

   $$\vec{y} = [ 0, 1, 0, 0 ]$$

   即只在表示 B 的维度上的标签是1，而表示其它类别的维度上的标签是0。

   所以在上面的损失函数中，并不需要对单样本的K个分量求和，因为其中只有一个分量$y_j$是1，其它分量都是0，所以可以简化为：

   $$J(W) = - \frac{1}{m} \sum_{i=1}^m \frac{e^{z_{mj}}}{\sum_{j=1}^K e^{z_{mj}}} \quad, \qquad (y_{mj}=1) \tag {4-46}$$

   其中 $z_{mj} = \vec{w_j} \vec{x}+b $

   这种交叉熵损失和softmax函数组合的形式，也被称为 softmax loss。

4.7 广义线性模型(Generalized Linear Model)

在统计学中，广义线性模型（GLM）是普通线性回归的灵活推广。在前面提到的普通线性回归、逻辑回归、多元逻辑回归等模型，其实可以看作广义线性模型的一种情况。

4.7.1 指数分布族(Exponential Family)

因为广义线性模型用到了指数分布族的相关知识，所以需要先了解 指数分布族(Exponential Family) 的相关概念。

指数分布族指的是，概率函数可以表示为如下形式的概率分布集合：

$$\begin{aligned} p(y;\eta) &= b(y) \exp(\eta^T T(y) - \alpha(\eta)) \\ &= b(y) e^{\eta^T T(y) - \alpha(\eta)} \end{aligned} \tag {4-47}$$

其中：

• $\eta$ 被称为自然参数(natural parameter)
• $T(y)$ 被称为是充分统计量(sufficient statistic)（一般情况下可以将$T(y)=y$）
• $\alpha(\eta)$ 被称为是对数划分函数(log partition function) ($e^{-\alpha(\eta)}$本质上起着归一化常数的作用，确保$p(y;\eta)$在$y$上求和/积分 为 1)

确定 $T$、$\alpha$、$b$ 三个函数后，就可以得到一个以 $\eta$ 为参数的概率分布 $p(y;\eta)$。

4.7.2 指数分布族示例

1. 高斯分布

   高斯分布的概率密度函数为：

   $$p(y;\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(y-\mu)^2}{2\sigma^2}} \tag {4-48}$$

   为了简化问题，假设其方差为 $\sigma^2=1$，则其概率密度函数简化为：

   $$p(y;\mu) = \frac{1}{\sqrt{2\pi}} e^{-\frac{(y-\mu)^2}{2}} \tag {4-49}$$

   将其向着指数分布族的形式转化：

   $$\begin{aligned} p(y;\mu) &= \frac{1}{\sqrt{2\pi}} e^{-\frac{(y-\mu)^2}{2}}\\ &= \frac{1}{\sqrt{2\pi}} \exp{-\frac{(y^2-2 \mu y+ \mu^2)}{2}} \\ &= \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} \exp({\eta y-\frac{\mu^2}{2}}) \\ &= \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} e^{({\mu y} -\frac{\mu^2}{2} )} \\ \end{aligned} \tag {4-50}$$

   如果令：

   $$\begin{aligned} b(y) &= \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} \\ \eta &= \mu \\ T(y) &= y \\ \alpha(\eta) &= \frac{\mu^2}{2} = \frac{\eta^2}{2} \\ \end{aligned} \tag {4-51}$$

   则高斯分布的概率密度函数就能表示为指数分布族的形式，所以高斯分布可以认为是指数分布族中的一种情况。
   
   

2. 伯努利分布
   伯努利分布又名两点分布或者0-1分布，概率函数为：

   $$p(y;\mu) = \mu^y (1-\mu)^{1-y} \tag {4-52}$$

   其中 $\mu$ 表示成功概率，$y$ 表示实验结果。

   伯努利分布也可以表示为指数分布族的形式：

   $$\begin{aligned} p(y;\mu) &= \mu^y (1-\mu)^{1-y} \\ &= \exp (yln\mu + (1-y)ln(1-\mu) ) \\ &= \exp (yln(\frac{\mu}{1-\mu} )+ ln(1-\mu) ) \\ &= e^{yln(\frac{\mu}{1-\mu} )+ ln(1-\mu)} \end{aligned} \tag {4-53}$$

   其中：

   $$\begin{aligned} b(y) &= 1 \\ \eta &= ln(\frac{\mu}{1-\mu} ) \\ T(y) &= y \\ \alpha(\eta) &= -\ln(1-\mu) = \ln(1+e^{\eta}) \\ \end{aligned} \tag {4-54}$$

4.7.2 广义线性模型

广义线性模型建立在3个前提假设上：

• 自然参数 $\eta$ 与 $x$ 是线性相关： $ \eta = X\beta + \epsilon $,
  此时称 $\eta$ 为线性预测子；

• $y$ 的估计值就是 $P(y|x,\beta)$ 的期望值。
  如果用 $h(x,\beta)$ 表示 $y$ 的估计值，这一假设写作 $h(x,\beta) = E[y|x,\beta]$
  也可以用所谓的链接函数 $g(\cdot)$ 表示： $ E[y|x,\beta] = \mu = g^{-1}(\eta) = g^{-1}(X\beta) $， 链接函数解释了线性预测子与分布期望值的关系；

• $y$ 的概率密度函数 $Pr(y|x,\beta)$ 满足指数分布族的条件。

1. 推导线性回归
   对于普通线性回归模型，我们认为 $y$ 服从正态分布，则

   $$\begin{aligned} h(x,\beta) &= E[y|x,\beta] \\ &= \mu \\ &= \eta \\ &= X\beta \end{aligned}$$

2. 推导逻辑回归
   对于逻辑回归模型，我们认为 $y$ 服从伯努利分布，则

   $$\begin{aligned} h(x,\beta) &= E[y|x,\beta] \\ &= \mu \\ &= \frac{1}{1+e^{-\eta}} \\ &= \frac{1}{1+e^{-(X\beta)}} \\ \end{aligned}$$

   而且对于伯努利分布, 其期望就是等于事件发生的概率，即

   $$E[y|x,\beta] = \mu = P(y=1|x,\beta)$$

   所以用Sigmoid函数映射后的输出，就是可以用来作为二分类时为正样本的概率。
   
   

3. 更多的线性回归推导

   这里截图了 Wikipedia 的广义线性模型的页面，可以参考:Generalized_linear_model