4 线性模型—(中)

4.2 局部加权线性回归(Locally Weighted Linear Regression)

4.2.1 局部加权线性回归的引入

上一篇引入线性回归问题时，示例数据 “外卖配送时间” 的散点图如下所示：

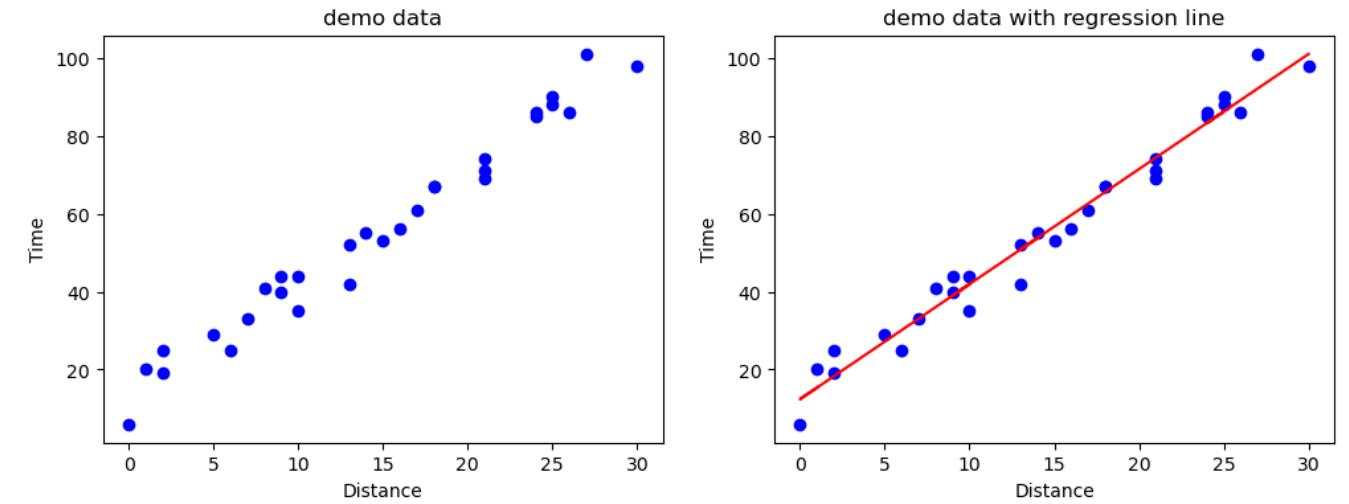
从图中的数据分布来看，使用线性回归模型基本上是没太大问题的，因为数据大致还是呈现线性分布的；虽然并不能保证所有的点都落在最后的拟合直线上，但是整体的趋势还是对的。

那么如果数据的分布并不是呈现完美的线性分布，如下图所示，用线性回归(Linear Regression)拟合出的直线，虽然依然在大趋势上是符合数据分布的，但是与上图中相比，下图中有些区域的点与拟合直线之间存在的偏差就有点明显的大了。

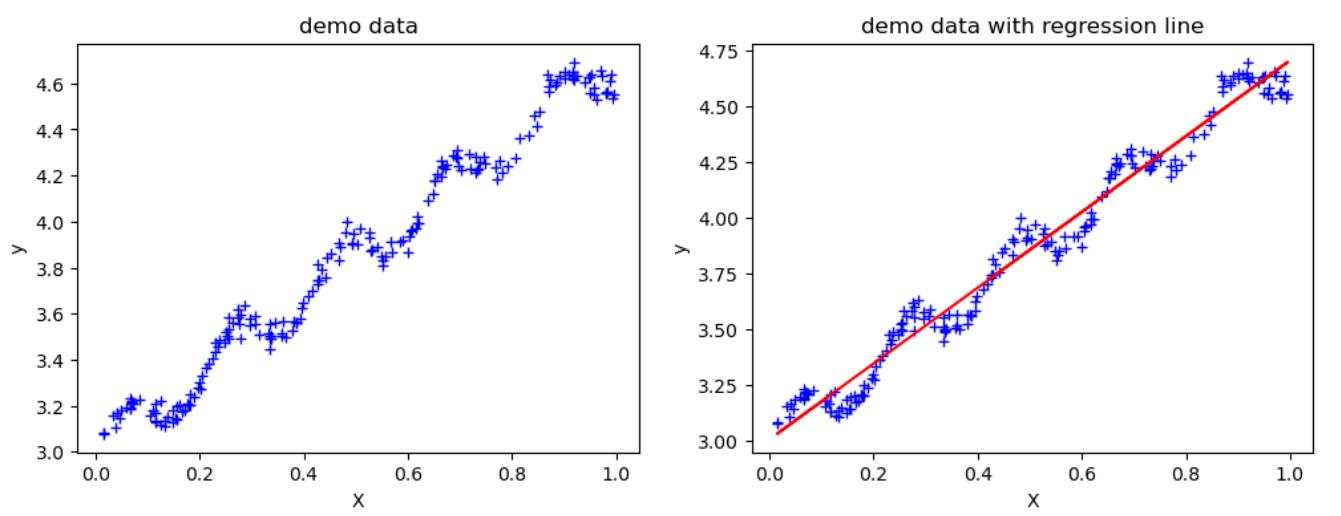
那么，有没有一种方法，能够对数据分布不规则的地方，其对应的线性回归参数能稍微有些变化，使得拟合结果能够更贴近训练数据呢？

局部加权线性回归就是解决此类，线性回归模型在训练集上欠拟合的情况。

4.2.2 局部加权线性回归的原理

因为在局部加权线性回归中涉及到权重的计算，所以为了与上一节讲到的线性回归的参数作区分，将权重记为 $\alpha $。

则普通线性回归，或者说标准线性回归的函数定义以及损失函数如下：

$h_w(x) = \sum_{i=0}^n w_i x_i = w^Tx \quad OR \quad x^Tw, \tag{4-9}$ $J(w) = \sum_{i=1}^m(h_w(x^{(i)})-y^{(i)})^2, \tag{4-10}$

在局部加权线性回归中，额外学习一个权重的参数 $\alpha $ , 即每个样本 $x^{(i)}$ 都有一个与其对应的权重 $\alpha^{(i)}$，设 $\alpha $ 是一个对角线矩阵：

$\alpha = \begin{bmatrix} \alpha^{(1)} \quad \quad \quad \quad \quad \\ \quad \alpha^{(2)} \quad \quad \quad \quad \\ \quad \quad \cdots \quad \quad \quad \\ \quad \quad \quad \alpha^{(i)} \quad \quad \\ \quad \quad \quad \quad \cdots \quad \\ \quad \quad \quad \quad \quad \alpha^{(m)} \\ \end{bmatrix}$

用这个权重值 $\alpha$ 来控制各个样本对于拟合模型参数 $w$ 时的贡献度。那么我们就可以在线性回归的损失函数中加入 $\alpha$ ，这样一来，就意味着不同的样本，对于损失函数的贡献程度是不一样的，进而对于参数的贡献度就是不一样的：

$J(w) = \sum_{i=1}^m \alpha^{(i)} (h_w(x^{(i)})-y^{(i)})^2, \tag{4-11}$

将其写成矩阵形式：

$J(w) = \alpha ||Xw-\vec{y}||^2 = (Xw-\vec{y})^T \alpha (Xw-\vec{y}), \tag{4-12}$

同样令其导数为0时，得到的等式为：

$X^T \alpha Xw = X^T \alpha \vec{y} \tag{4-13}$

最终参数$w$的值可以表示为：

$w = (X^T \alpha X)^{-1} X^T \alpha \vec{y} \tag{4-14}$

由此可见，参数 $w$ 的值与 $\alpha$ 有关。

那么如何来定义每个样本 $x^{(i)}$ 对应的权重 $\alpha^{(i)}$ 呢？我们使用该权重的目的是控制每个样本对参数 $w$ 的影响程度。

显然当 $ \alpha^{(i)} $ 取值较大时，该样本 $x^{(i)}$ 对参数 $w$ 的影响程度较大，反之亦然（因为影响了该样本的损失函数值）。

那么什么时候该让样本 $x^{(i)}$ 的影响度大一点呢？试想，如果此时有一个待预测样本 $x^{(new)}$，如果它离样本 $x^{(p)}$ 较近，而离样本 $x^{(q)}$ 较远，那么显然应该让 $x^{(p)}$ 产生更大的贡献，来拟合参数 $w$，进而来预测 $x^{(new)}$ 的输出值。

所以，对于待预测样本，离它最近的样本 $x^{(i)}$ 产生的贡献度应该最大，而离它最远的样本 $x^{(i)}$ 产生的贡献度应该最小。这也正是局部加权四个字想表达的意思，即对于一个待预测样本，只让距离其较近的（局部）一些训练样本对其施加多一点的影响。可以用以下公式来描述这种关系：

$\alpha^{(i)} = \exp{ (\frac{|x^{(i)}-x|}{-2k^2} )}\tag{4-15}$

该函数是高斯核函数，其中 $k$ 为超参数，$x$ 为待预测样本，$x^{(i)}$ 为训练样本；$k$ 为超参数，可以手动调整，用来控制权重的缩放程度。

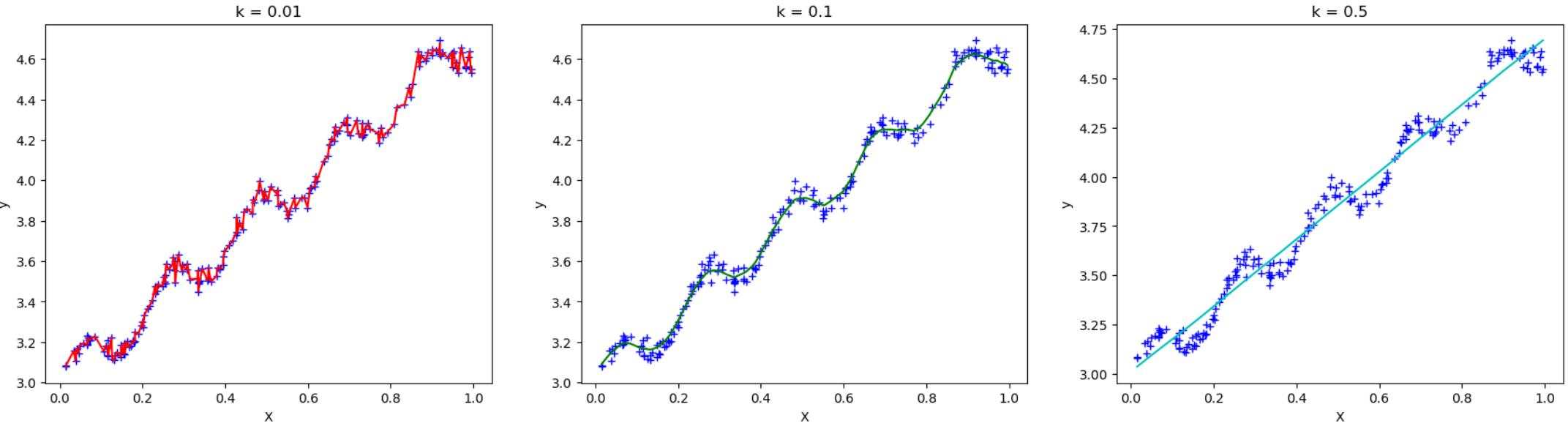
如上图所示，采用不同的 $k$ 值，对权重的影响程度不同:

$k$ 值越小，远处的点权重缩小幅度较大，趋近于0，所以数据点受近处局部影响更大，容易过拟合。
$k$ 值适中，远处的点权重缩小幅度合适，能够较好的拟合数据。
$k$ 值越大，远处的点权重缩小有限，趋近于1，接近LS。

4.2.3 非参数化模型

局部加权线性回归，是非参数化模型，也就是说，参数 $w$ 并不是一直固定的。

普通线性回归，利用训练数据训练完成之后，参数 $w$ 就不会再改变，所以是参数化模型；
局部加权线性回归，对于每一个待预测样本，因为并不知道其和训练数据各个样本的距离，所以都会重新计算样本权重 $\alpha$。也就是每一次都要遍历所有的样本 $x^{(i)}$ 计算对应的 $\alpha^{(i)}$，所以局部加权线性回归的计算量会比普通线性回归要大很多。

4.3 岭回归(Ridge Regression)

4.3.1 岭回归的提出

之前讲过使用最小二乘法(LS)来拟合线性回归模型时，使用正规方程组来求解的。当时说过，要使用正规方程组来求解参数，需要保证所有的样本是线性无关的，即不存在多重共线性。如此才能满足正规矩阵（格拉姆矩阵）可逆的条件，从而得到唯一解。
但是，在实际应用中，样本往往存在多重共线性，即存在线性相关的情况，并不能很好地保证正规矩阵可逆，所以此时使用最小二乘法进行拟合的模型，可能就会不太合适。

4.3.2 岭回归的原理

样本存在多重共线性时，正规矩阵 $ (X^TX) $ 不可逆，我们现在来将正规矩阵 $ (X^TX) $ 进行改造：
对于正规矩阵 $ (X^TX) $ ，在其对角线上的元素都加上一个正实数 $\lambda$ ，即 $ (X^TX) + \lambda I$。得到的这个矩阵 $ (X^TX + \lambda I) $ 一定是可逆的！
简单的说一下为什么：

首先， $ (X^TX) $ 是实对称矩阵，这个很容易理解；
实对称矩阵的性质如下，可以查询百度百科的词条【半正定矩阵】：
关于特征值非负的证明：
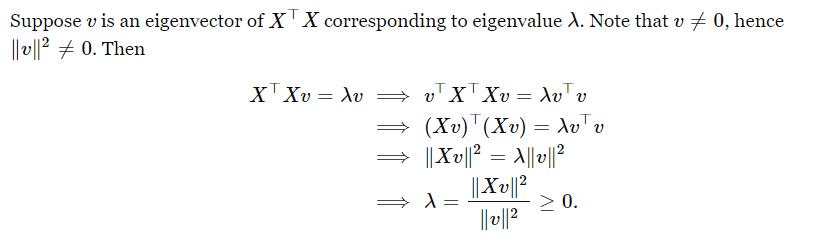
然后，实对称矩阵也必定可以相似对角化，可以查询百度百科词条【实对称矩阵】：
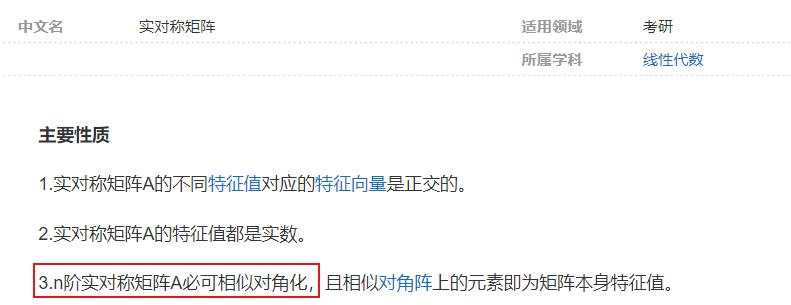
所以，给一个实对称矩阵，在对角元素上加上一个正实数 $ \lambda $，它仍然是一个实对称矩阵（因为除对角线外的元素并未变化，所以依然以对角线对称）：
则其最小特征值就至少是 $ \lambda $，若 $ \lambda > 0 $ 就说明该实对称矩阵的最小特征值大于0；
故：特征值大于0的n阶实对称矩阵，是正定矩阵，即矩阵可逆。可以查询百度百科词条【正定矩阵】：

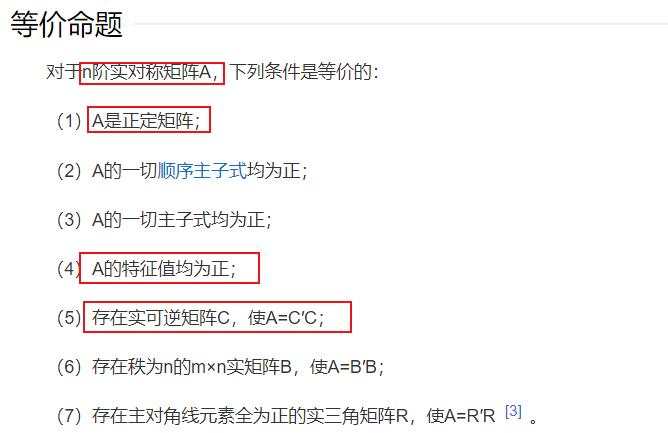
综上： 矩阵 $ (X^TX + \lambda I) $ 一定是可逆的！

而岭回归名字的由来其实就是因为在正规矩阵的基础上加了一个 $\lambda I $矩阵，“岭”就是指的这个对角线。 $\lambda I = \begin{bmatrix} \lambda \quad \quad \quad \quad \quad \\ \quad \lambda \quad \quad \quad \quad \\ \quad \quad \cdots \quad \quad \quad \\ \quad \quad \quad \lambda \quad \quad \\ \quad \quad \quad \quad \cdots \quad \\ \quad \quad \quad \quad \quad \lambda \\ \end{bmatrix}$

4.3.3 岭回归的优化策略

故对正规矩阵做修改之后，依然可以沿用最小二乘法的思想，来求解修改后的方程组，得到唯一解。
正规方程组式（4-4-4）可以改为：

$X^T \vec{y} = (X^TX + \lambda I) w, \tag{4-16}$

而这个式子本身应当是对损失函数求 $ w $ 的导数，令导数为0 得到的等式，所以可以得到其导数的改写形式：

$\frac{\partial J(w)}{\partial w} = (X^TX + \lambda I) w - X^T \vec{y} \tag{4-17}$

事实上，我们只需要将损失函数写为以下形式，就能得到上面的导数形式：

$J(w) = ||Xw-\vec{y}||^2 + \frac{\lambda}{2}||w||^2 \tag{4-18-1}$

可以将 $\frac{1}{2} $ 去掉，或者说融合进 $ \lambda $ 中，得到：

$J(w) = ||Xw-\vec{y}||^2 + \lambda||w||^2 \tag{4-18-2}$

式（4-18-2）就是岭回归(Ridge Regression)的损失函数 。

再此基础之上，可以像普通线性回归那样有两种优化策略求解 $ w $：

直接解正规方程组：

$w = (X^TX + \lambda I)^{-1} X^T \vec{y} \tag{4-19}$

使用梯度下降法：

$w = w - \alpha \frac{\partial J(w)}{\partial w} \tag{4-20}$

4.3.3 岭回归的另一种理解

我们看到，岭回归的损失函数是：

$J(w) = ||Xw-\vec{y}||^2 + \lambda||w||^2 \tag{4-18-2}$

其实就是在最小二乘损失函数后面多了一个惩罚项，它的目的是希望参数 $w$ 的 L2 范数小，这其实就是正则化。

正则化：一种防止模型过拟合的策略，在损失函数后面加入一个正则化项，使得模型在训练的时候更加健壮，防止过拟合。

L2范数的定义：

$||w||_2 = \sum_{i=1}^n |w_i|^2 \tag{4-21}$

所以它会防止 $w_i$ 的平方值过大，那么因变量 $y$ 的变化幅度就会比较缓慢，从而使得模型更加稳定。

在平时，一般不是很好判断训练样本是否具有多重共线性；其实只要发现训练样本的规模不是很大，那么就可以考虑使用岭回归。因为训练样本较小时，普通线性回归容易对训练样本产生过拟合，而岭回归因为使用了正则化，可以避免过拟合。

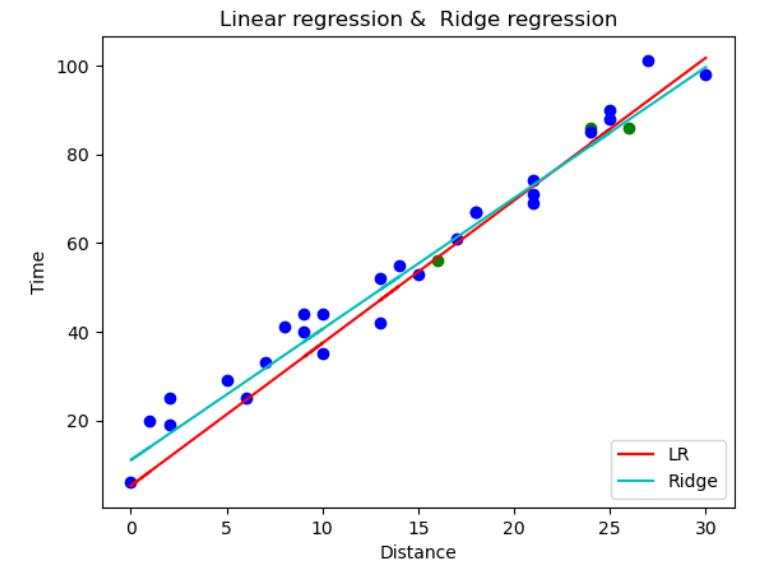
下面的示例，我们故意只使用几个样本点来进行训练（绿色的点是训练样本），蓝色的点是测试样本（相对于训练样本的规模来说，测试样本规模更大），分别使用普通线性回归和岭回归，对结果进行对比；会发现岭回归的拟合曲线更加贴合测试集样本。

4.4 拉索回归(Lasso Regression)

4.4.1 拉索回归的原理

Lasso回归的全称是 Least Absolute Shrinkage and Selection Operator 回归，中文名是最小绝对值收缩和选择算子回归。这个名字乍一听有点复杂，但是了解了它的原理和作用之后就容易理解了。

Lasso回归的损失函数是：

$J(w) = ||Xw-\vec{y}||^2 + \lambda||w|| \tag{4-22}$

和岭回归相似，同样是在最小二乘损失函数后面多了一个惩罚项，只不过该惩罚项是 $ \lambda||w|| $ ，它的目的是希望参数 $w$ 的 L1 范数尽量小。 L1 范数就是绝对值，所以 Lasso 回归就是对系数进行绝对值压缩。

L1 范数定义：

$||w||_1 = \sum_{i=1}^n |w_i| \tag{4-23}$

这就是其名字中 最小绝对值收缩(Least Absolute Shrinkage) 的含义。

4.4.2 拉索回归的优化策略

Lasso回归的损失函数中有绝对值项，所以其导函数并不是在所有位置连续可导的，所以之前的通过求导的方法来解最优参数的方法都不使用。
使用 坐标下降(Coordinate Descent) 算法和 最小角回归法。

挖坑、待填。

4.4.3 拉索回归和岭回归的区别

Ridge 回归和 Lasso 回归都是正则化，但是岭回归是 L2 正则化，Lasso 回归是 L1 正则化。 这就决定了一个很重要的特性：

如果最小化Lasso回归的损失函数，最后得到损失函数极小值时，参数 $w$ 的一些分量是可以被压缩至0的;
如果最小化Ridge回归的损失函数，最后得到损失函数极小值时，参数 $w$ 的各个分量都接近于0，但是不能被压缩至0。（这里注意不要误解，不是说 $w$ 的分量不能在优化过程中取0，而是取0的时候，一定还达不到极小值；当到达极小值的时候，$w$ 的所有分量是取不到0的。）

以上这个特性主要是由于L1范数和L2范数的不同决定的，网上有很多资料，一般都是从损失函数等高线的角度去解释的，如下图¹所示，在这里不赘述。推荐这一系列文章² ³。

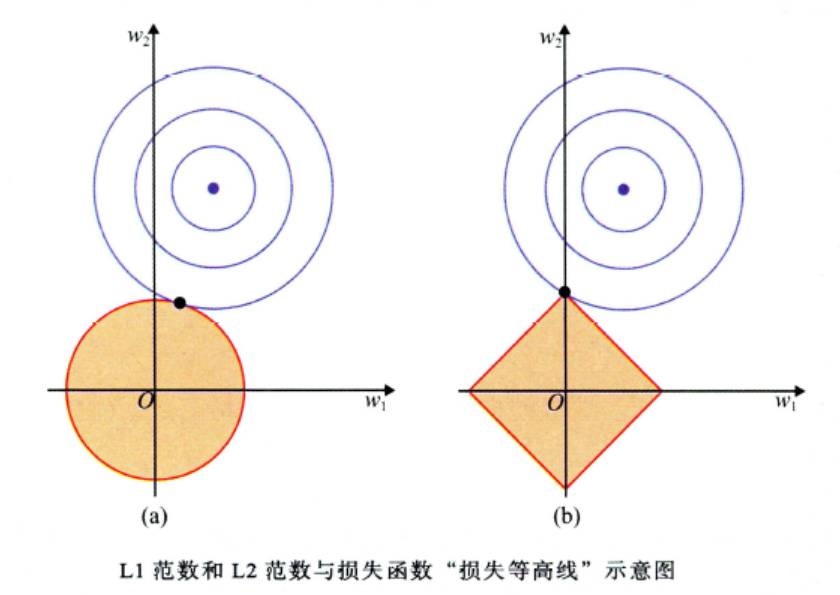
如果真的想深入探究一下L1正则化和L2正则化的一些应用，可以看一下吴恩达的这篇论文⁴，不过这篇文章没有图片，很多数学公式，符合吴老师的风格。

所以，Lasso 回归能够将参数中一些不重要的参数压缩至0，表示对应样本那个维度的特征不重要，也就是说在拟合模型的过程中，可以剔除样本的一些不重要特征，起到了特征筛选的作用。这就是名字中选择(Selection)的含义。

4.5 弹性网络回归(Elastic Net Regression)

4.5.1 弹性网络回归的损失函数

就是同时考虑 L1正则化和 L2正则化，其损失函数定义如下：

$\mathcal{L}(w) = ||Xw-y||^2 + \rho \alpha ||w|| + (1-\rho) \alpha||w||^2 \tag{4-24}$

其中，

$\rho$ 被称为 $L1_ratio$，且 $0 <= L1_ratio <= 1$ ，该参数用来控制模型是更侧重于 L1 正则化还是 L2 正则化。$\rho=1$ 时就只考虑L1正则化，相当于Lasso回归；$\rho=0$ 时就只考虑L2正则化，相当于Ridge回归。
$\alpha$ 是正则化系数，控制正则化的惩罚力度；如果 $\alpha=0$ 则不进行正则化，退化为普通的线性回归。